Verificare e convalidare queste equazioni è fondamentale per infondere fiducia nei modelli climatici. Sebbene una certa discrepanza tra le previsioni del modello e le osservazioni effettive sia inevitabile, l'obiettivo è che le configurazioni specifiche del modello convergano verso la soluzione corretta alla velocità attesa dagli scienziati.

I modelli matematici continui devono subire un processo chiamato discretizzazione, che li converte in forme che possono essere risolte numericamente dai computer. I casi di test possono aiutare con la verifica complessiva di un modello estraendo sottoinsiemi di equazioni discretizzate e verificando ciascun termine.

Misurare la velocità con cui le soluzioni numeriche di questi casi di test convergono verso le soluzioni esatte (il che significa che gli errori si avvicinano allo zero) è il metodo gold standard per la verifica del modello. I tassi di convergenza in linea con le aspettative teoriche sono la migliore garanzia che le equazioni discretizzate siano codificate correttamente.

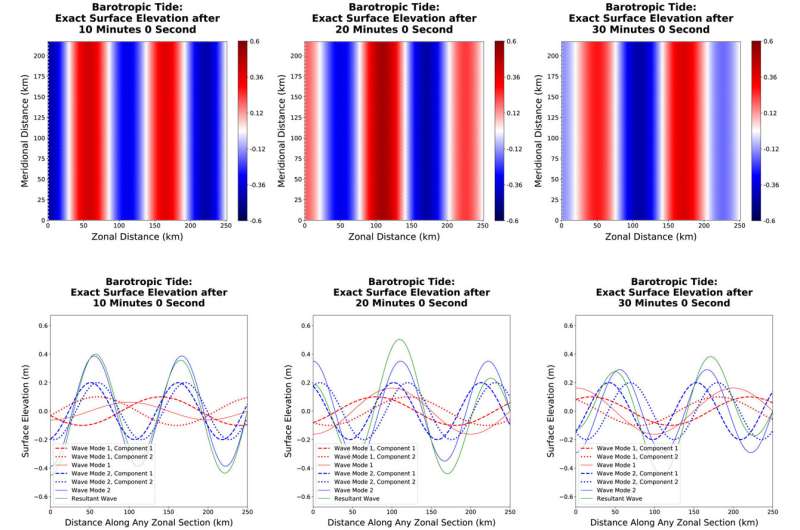
Per motivi di efficienza computazionale, i modelli oceanici in genere dividono le loro equazioni governative in una componente baroclina 3D che modella le onde gravitazionali interne lente e le correnti oceaniche e una componente barotropica 2D che modella le onde gravitazionali superficiali veloci. La componente barotropica assume la forma di equazioni di acque poco profonde. Siddhartha Bishnu e colleghi presentano una raccolta di casi di prova incentrati su queste equazioni. La ricerca è pubblicata sul Journal of Advances in Modeling Earth Systems .

Per sviluppare i casi di test, i ricercatori hanno attinto alla loro esperienza nello sviluppo del Model for Prediction Across Scales–Ocean (MPAS–Ocean), che viene utilizzato per simulare l’attività oceanica e studiare come viene influenzata dai cambiamenti climatici di origine antropica. Gli autori notano che i loro casi di test hanno lo scopo di verificare l'accuratezza del modello (per garantire che le equazioni del modello discretizzato siano implementate correttamente), piuttosto che convalidare i risultati (per garantire che le previsioni del modello assomiglino alle osservazioni del mondo reale).

I ricercatori hanno esaminato i fondamenti teorici delle equazioni delle acque poco profonde insieme ai metodi di discretizzazione, hanno offerto una panoramica dei casi di test per garantire la riproducibilità e hanno dimostrato che i tassi di convergenza corrispondono alle previsioni previste.

Questi casi di test consentiranno ad altri ricercatori di valutare i componenti dei loro modelli senza la necessità di un'eccessiva potenza di calcolo, scrivono gli autori. Inoltre, i casi di test potrebbero essere utili per problemi di fluidodinamica più ampi e servire come strumenti didattici per lo studio e lo sviluppo di modelli oceanici.