I ricercatori hanno scoperto che le cellule epiteliali, quelle che ricoprono la superficie di molti organi umani, utilizzano una nuova forma geometrica, lo scuoide, così i tessuti possono curvarsi. Università di Siviglia

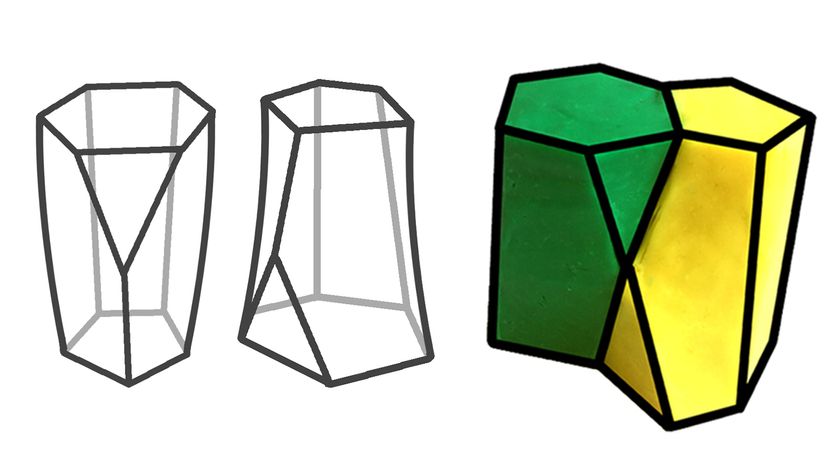
A meno che tu non abbia vissuto sotto uno sferoide oblungo, probabilmente hai sentito parlare dell'ultima scoperta in fatto di forme:lo scutoide. Un team di biologi spagnoli dell'Università di Siviglia ha modellato lo scutoide per determinare come le cellule epiteliali si uniscono per formare le barriere della pelle, organi e vasi sanguigni.

I ricercatori hanno semplicemente usato la matematica per ipotizzare una forma in natura, una forma necessaria per la costruzione di organismi multicellulari. Quando divenne chiaro che la forma era nuova per la geometria, gli diedero il nome dello scutello, la parte del torace di un coleottero che ricorda vagamente lo scutoide appena battezzato.

Nell'esempio dello scutoide, possiamo intuire molto sulla scoperta di nuove forme:da dove vengono e perché le cerchiamo per cominciare.

La forma più elementare di scoperta delle forme è semplicemente osservarle nel mondo naturale. L'esagono (un poligono a sei lati), ad esempio, si verifica in tutto, dalle bolle di sapone e dai favi alle nuvole di Saturno. Come ha esplorato lo scrittore Phillip Ball nell'articolo di Nautilus "Perché la natura preferisce gli esagoni, " spiega come sia una forma geometricamente ideale per una serie di funzioni. Come tale, l'esagono è emerso dalle interazioni fisiche e dall'evoluzione biologica. Gli umani sono appena arrivati ​​e l'hanno chiamato.

Altre forme sono meno comuni in natura ma emergono facilmente dalla geometria o persino dall'immaginazione disinformata. angoli retti, ad esempio, sono rari nel mondo naturale. Una passeggiata nella natura selvaggia non ti presenterà con quadrati e rettangoli. Infatti, la ricerca indica che potremmo invece essere programmati per preferire le curve naturali alle linee rette. Eppure costruiamo ancora cubi e li usiamo per rifare il mondo.

C'è una disconnessione, però, tra i tipi di forme che possono essere concettualizzate e quelle che possono essere trovate o riprodotte nella natura. Cerchi perfetti, ad esempio, non esistono nel nostro regno materiale. Da un punto di vista puramente matematico, possiamo facilmente costruire un insieme di punti in un piano equidistanti da un dato punto. Ma, in realtà, anche i cerchi e le sfere più finemente realizzati non raggiungono la perfezione matematica. Anche i rotori giroscopici al quarzo costruiti per la Gravity Probe B della NASA sono ancora a meno di tre decimilionesimi di pollice dalla perfezione.

Lo scuroide, però, sembra esistere davvero. Potremmo non essere in grado di vedere esso, ma gli scienziati lo hanno modellato matematicamente come soluzione per un problema biologico. Come tale, se la scienza un giorno abbandonasse lo scuroide in favore di un'altra soluzione, la forma stessa continua ad esistere geometricamente.

Così, aggiornare, si possono scoprire le forme individuandole in natura, inferirne l'esistenza in natura o attraverso un esercizio di matematica pura. È raro di questi tempi, ma i cacciatori di forme occasionalmente scoprono un nuovo tipo di pentagono o persino una nuova classe di forme solide.

Quindi con tutti i mezzi, vai là fuori e vedi cosa riesci a trovare, anche se tieni presente che abbiamo già alcune forme matematiche in archivio. Il dodecaedro trapezo-rombico è già stato preso e Clickhole ha i privilegi del Triquandle.

Ora è impossibile

Le illusioni ottiche come il triangolo di Penrose sfruttano le stesse tendenze visive che rendono le lettere al contrario un errore così facile nella scuola elementare. UN P e un Q sono nettamente diversi sulla carta, ma se le interpretiamo come immagini 3D, allora sono semplicemente due viste dello stesso oggetto. Il triangolo di Penrose non può veramente esistere nello spazio 3D, ma lo percepiamo come un oggetto 3D e questa figura sconcertante è ancora composta nel forma di un triangolo. Ancora, come hanno dimostrato Lionel e Roger Penrose, tu Potere scoprire e nominare tali oggetti, anche se Oscar Reutersvärd l'ha creato anni prima.