Le sfere magnetiche forniscono strade entusiasmanti per esplorare molti fenomeni fondamentali della fisica. Possono essere assemblati a mano in catene e strutture più complesse e utilizzati per modellare le proprietà di materiali inestensibili che, come carta, deformarsi in determinate condizioni di carico.

Le sfere magnetiche impilate l'una sull'altra in catene verticali rimangono stabili, ma solo per determinate scelte di parametri salienti. Il professor Eliot Fried e il dottor Johannes Schönke dell'Okinawa Institute of Science and Technology Graduate University (OIST) hanno esaminato la lunghezza massima di una catena di sfere magnetiche che possono essere bilanciate verticalmente senza rovesciarsi, un fenomeno semplice ma importante legato alla stabilità delle sfere magnetiche Catene. Utilizzando la teoria e l'analisi matematica in combinazione con dati sperimentali, hanno determinato i valori dei parametri critici in corrispondenza dei quali le catene perdono stabilità in varie circostanze.

Le scoperte, pubblicato in Atti della Royal Society of London Serie A , potrebbe fornire informazioni sulla stabilità dei materiali non elastici utilizzati nella progettazione architettonica su larga scala. Questo ha molte applicazioni pratiche nella costruzione, dai camini in cemento delle centrali elettriche ai gusci esterni dei razzi.

Primo, consideravano un'unica catena fissata alla sua base composta da sfere magnetiche di 5 mm di diametro, ciascuno del peso di 0,5 grammi e avente una densità di flusso magnetico di 1,19 Tesla (T). Una catena di nove palline rimane stabile, ma una catena di 10 palline si piega sotto il suo stesso peso.

"È una competizione tra forza magnetica e gravità, " dice il dottor Schönke. "Quando la catena raggiunge le 10 palline, la gravità vince sulla forza magnetica, e la catena perde stabilità."

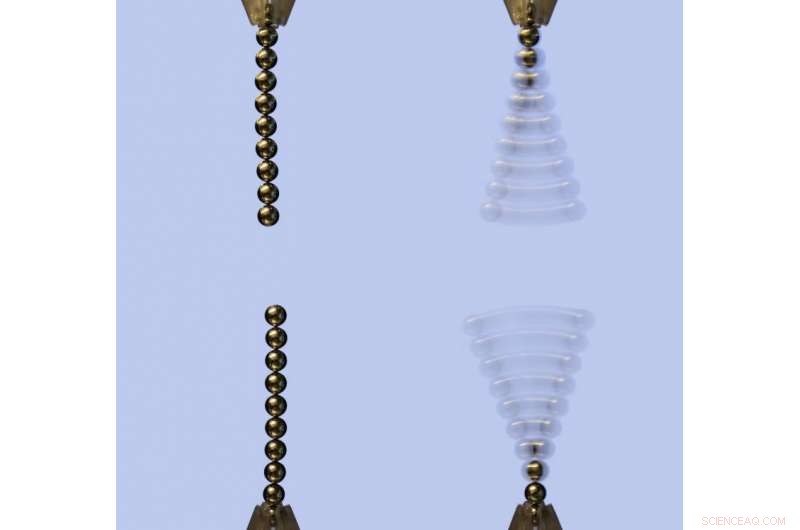
Prossimo, il team ha esaminato il caso di due catene, uno è attaccato al suolo e l'altro appeso sopra con uno spazio di lunghezza prescritta nel mezzo. Quando i campi magnetici erano allineati in modo tale che la catena superiore e la catena inferiore fossero attratte magneticamente l'una dall'altra, la catena superiore stabilizzava una catena inferiore di 10 palline di lunghezza. In altre parole, la presenza di una catena magnetica superiore aumenta la lunghezza alla quale una catena bloccata alla sua base rimane stabile.

"Con l'aumentare del numero di sfere magnetiche nella catena inferiore, lo spazio tra le catene superiore e inferiore deve essere ridotto affinché la catena inferiore rimanga stabile, " spiega il dottor Schönke.

Anche se la catena inferiore non è fissata, l'interazione magnetica con la catena superiore fornisce stabilità - uno scenario impossibile per una singola catena non fissata. Però, in questo caso, se la distanza tra le catene superiore e inferiore è troppo piccola, la catena inferiore non fissata si solleva e si attacca alla catena superiore.

Nella configurazione sperimentale finale, i ricercatori hanno invertito l'orientamento delle sfere magnetiche nella catena superiore in modo che la direzione del campo magnetico della catena superiore si opponesse a quella della catena inferiore fissa. A causa della risultante forza di repulsione tra le due catene, la catena inferiore rimane stabile solo con otto sfere, una sfera in meno di una catena fissa singola stabile e due sfere in meno di una catena inferiore fissa stabile attratte da una catena superiore sospesa.

"Abbiamo scoperto che la stabilità delle catene magnetiche è determinata dal numero di palline in una catena, la dimensione dello spazio tra la catena superiore e inferiore, e la forza delle forze magnetiche rispetto alla gravità, "dice il professor Fried, che dirige l'Unità Matematica Soft Matter dell'OIST.

"Può sembrare un po' divertente con i magneti giocattolo, ma infatti, abbiamo eseguito calcoli matematici non banali che ci permettono di spiegare la stabilità delle catene magnetiche con estrema precisione, " dice il dottor Schönke.

Questi risultati forniscono una base su cui studiare strutture più complesse di sfere magnetiche, come tubi cilindrici costituiti da anelli circolari impilati. Se gli anelli sono impacchettati in modo tale che ogni pallina sia in contatto solo con i suoi quattro immediati vicini, può essere deformato in molti modi.

Rispetto agli anelli imballati quadrati, anelli esagonali in cui ogni pallina è in contatto con le sue sei vicine, sono più stabili. Mantenere le connessioni tra le sfere in questo modo crea un sistema incapace di estensione o contrazione. Come tale, le strutture così configurate forniscono un modello per la comprensione di materiali inestensibili come la carta.

"Uno dei prossimi passi è condurre simulazioni più dinamiche utilizzando tubi cilindrici di sfere magnetiche e determinare i valori dei parametri critici in corrispondenza dei quali le strutture configurate in questo modo perdono stabilità, " dice il dottor Schönke.