
Questo film di sapone contenuto all'interno di un'asta di metallo ha giunzioni in cui più film di sapone si incontrano. Nel 2014, La prof.ssa Jenny Harrison dell'UC Berkley ha esteso la soluzione al problema del Plateau per tenere conto di forme di pellicola di sapone più complicate come questa. Credito:Okinawa Institute of Science and Technology
Spesso usato per il divertimento dei bambini, le bolle di sapone sono delicate, pellicole che riflettono la luce che in genere durano solo pochi secondi prima di scoppiare. Ma al di là del loro valore per intrattenere, le bolle di sapone sono esempi fisici del ricco problema matematico delle superfici minime; assumono la forma della superficie minore possibile, contenente un dato volume. I ricercatori dell'Okinawa Institute of Science and Technology Graduate University (OIST) hanno recentemente elaborato la soluzione a un problema matematico, noto come problema di Kirchhoff-Plateau, che è semplicemente illustrato da pellicole di sapone che si estendono su anelli flessibili.
"La nostra soluzione del problema di Kirchhoff-Plateau porta bellissimi risultati matematici vicini a ciò che accade nel mondo fisico, " dice il dottor Giulio Giusteri, coautore del documento che è stato recentemente pubblicato sul Journal of Nonlinear Science. Il dott. Giusteri ha lavorato con il professor Eliot Fried, che dirige l'Unità Matematica Soft Matter dell'OIST, e il Dott. Luca Lussardi dell'Università Cattolica del Sacro Cuore in Italia.
La domanda a cui risponde il team è una variante del "problema dell'altopiano", un secolare problema matematico, prende il nome dal fisico belga del XIX secolo, Giuseppe Altopiano. Plateau ha ipotizzato che quando si immerge un telaio di filo rigido in una soluzione di sapone, la superficie della pellicola di sapone formata sul telaio rappresenta un'area minima matematicamente possibile, non importa la forma del telaio.
La prima soluzione soddisfacente per il problema del Plateau è stata fornita nel XX secolo, dal matematico americano Jesse Douglas, per il quale è stato insignito della Medaglia Fields nel 1936. Più recentemente, nel 2014, La professoressa Jenny Harrison dell'UC Berkeley ha esteso il lavoro di Douglas, fornendo una prova valida sotto ipotesi generali che includano, Per esempio, situazioni in cui sono presenti giunzioni in cui più film di sapone si incontrano.
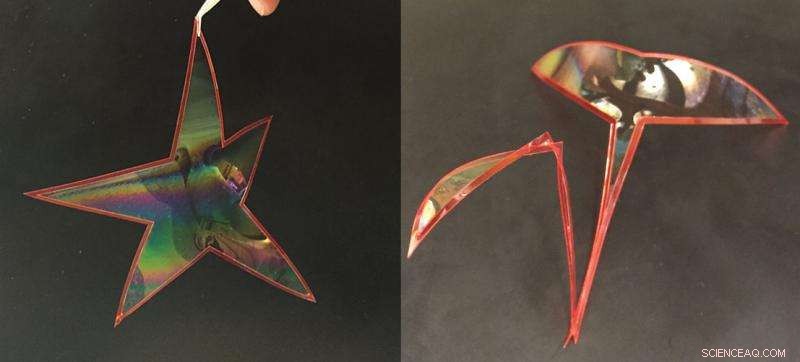
Le pellicole di sapone contenute all'interno di un'ansa flessibile esercitano una forza sull'ansa, facendogli cambiare forma. Ad esempio, lo stesso anello può formare una forma a stella oa cigno a seconda della tensione superficiale della pellicola di sapone. Credito:Okinawa Institute of Science and Technology
In contrasto con il problema del Plateau in cui un film di sapone si estende su un telaio fisso, il problema di Kirchhoff-Plateau riguarda le forme di equilibrio di film di sapone che attraversano anelli flessibili, fatto, ad esempio, della lenza, che può essere descritto utilizzando la teoria delle aste di Kirchhoff, un modello che fornisce un potente approccio per studiare la statica e la dinamica delle aste elastiche sottili. La complicazione è che un anello flessibile può cambiare forma in risposta alla forza esercitata dalla pellicola di sapone. Come tale, una soluzione al problema richiede di determinare non solo la forma della pellicola di sapone ma anche la forma dell'anello di delimitazione. In contrasto, la forma del confine nel problema del Plateau originale è nota perché è costituita da un filo rigido che rimane fissato contro le forze relativamente deboli della pellicola di sapone.
Un'ulteriore complicazione associata al problema di Kirchhoff-Plateau è che a differenza del problema Plateau originale in cui si presume che il confine sia unidimensionale, una bacchetta di Kirchhoff è un oggetto tridimensionale. Sebbene i filamenti come la lenza siano sottili, sono ordini di grandezza più spessi di una pellicola di sapone in equilibrio, il che significa che l'area della pellicola di sapone può cambiare a seconda del punto in cui la pellicola entra in contatto con l'anello.
I ricercatori hanno tradotto con successo tutti questi effetti fisici in termini matematici. Come spiega il prof. Fried:"Non importa quanto sia forte la competizione tra la tensione superficiale della pellicola di sapone e la risposta elastica del cappio, il sistema è sempre in grado di adattarsi per ottenere una configurazione di minor energia."
La soluzione del problema di Kirchhoff-Plateau non solo contribuisce alla comprensione dell'energia minimizzando le forme matematiche, ma può essere applicato anche ai sistemi biologici. Ad esempio, potrebbe aiutarci a capire come la forma di una proteina determina come interagisce e si lega a una superficie.
Il team sta ora lavorando su simulazioni al computer che, sulla base di questo modello matematico, può prevedere il comportamento dei sistemi fisici.