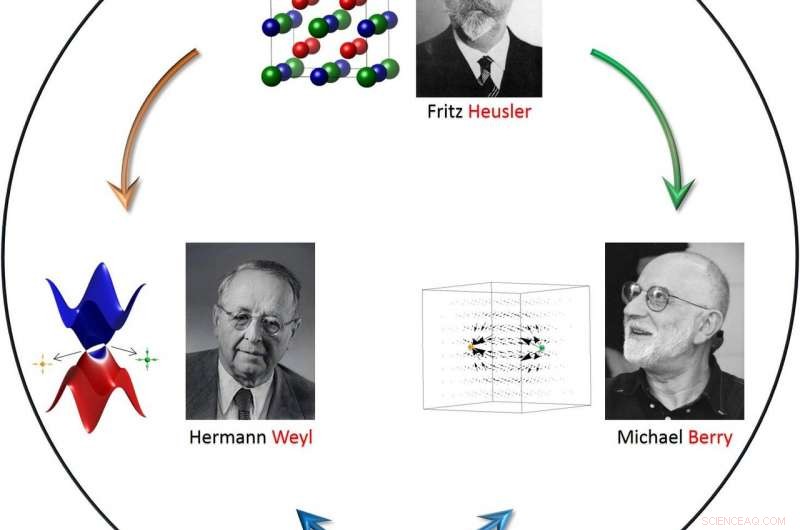
La figura mostra la connessione tra i fermioni di Weyl e la fase di Berry e la sua realizzazione nella famiglia di composti di Heusler. Nel pannello superiore, presentiamo una tipica disposizione atomica di una lega full-Heusler in cui le sfere rossa e blu sono metalli di transizione (come cobalto o ferro), con il rosso che è più elettropositivo del blu, e la sfera verde è un elemento del gruppo principale (come il silicio o il gallio). Nel pannello inferiore, viene visualizzata la struttura elettronica del semimetallo Weyl. I punti giallo e verde brillante presentano i monopoli magnetici in un semimetallo Weyl chirale e le frecce nere indicano la curvatura di Berry nello spazio del momento. Crediti:Heusler:Isabellenhütte GmbH &Co. KG;Weyl:ETH Zürich Bildarchiv;Berry:Michael Berry
Gli scienziati del Max Planck Institute Chemical Physics of Solids hanno scritto un documento di revisione sui materiali topologici magnetici nella famiglia dei composti di Heusler. La recensione spiega la connessione tra topologia, simmetria e magnetismo a un livello adatto a studenti universitari in fisica, chimica e scienza dei materiali con una conoscenza di base della fisica della materia condensata.
Fritz Heusler (1866-1947), Hermann Weyl (1885-1955) e Michael Berry (1941-) sono tre rinomati scienziati il cui lavoro ha portato a nuove e importanti intuizioni sulla scienza dei materiali, topologia e fisica della materia condensata. Questi tre campi della scienza si sono uniti di recente con la scoperta di nuove ed entusiasmanti proprietà quantistiche in nuove classi di materiali che potrebbero consentire nuove scienze, comprese le tecnologie informatiche e la catalisi.
Heusler è il nome dello scopritore di composti per lo più magnetici che interessavano molto tempo fa. Ma è stato recentemente scoperto che questi composti ospitano proprietà topologiche non banali che aprono un ampio campo di nuova fisica. Nascosti nella struttura a bande energetiche di questi materiali ci sono punti singolari che possono essere descritti con strumenti matematici che hanno origine da Weyl; questi punti sono associati alla scoperta di quasi-particelle che ora sono chiamate fermioni di Weyl. Non si trovano tra le particelle elementari della fisica delle alte energie, ma crediamo che esistano in materiali solidi e ne determinino la topologia. Il terzo nome Berry sta per gli effetti misurabili che rivelano la fisica a portata di mano. In determinate condizioni ben definite esiste un campo vettoriale, simile al campo magnetico, chiamata curvatura della bacca. Determina l'entità di una serie di effetti importanti, come l'effetto Hall anomalo e lo Spin Hall Effect. È l'arte dello sperimentatore modificare opportunamente i materiali per regolare la curvatura di Berry e rendere così visibile la topologia. In questa recensione viene fornito un gran numero di esempi per varie proprietà di simmetria dei composti di Heusler, una vasta classe di materiali che possono essere facilmente sintonizzati per visualizzare ferromagnetici, antiferromagnetico, ordine magnetico non collineare o compensato. Questi ordinamenti magnetici danno luogo a pronunciati effetti elettrici e termoelettrici le cui impronte digitali vengono scoperte e spiegate, comprese le strutture di spin a vortice simili a particelle, gli antiskyrmioni tipici di un certo sottoinsieme di composti di Heusler.
Considerando il gran numero di composti inorganici esistenti e il gran numero di materiali topologici non magnetici recentemente proposti, I composti di Heusler fungono da sistema modello per la comprensione e l'impatto del magnetismo sulla topologia. Rompere la simmetria di inversione del tempo tramite il magnetismo o un campo magnetico esterno può portare a effetti ancora maggiori rispetto ai materiali non magnetici basati sulla grande separazione tra punti Weyl di diverse chiralità. Sulla base di uno studio sistematico dei materiali di Heusler, prevediamo che ci sia un numero enorme di materiali topologici magnetici in attesa di essere scoperti.
Per quanto riguarda le candidature, il grande effetto Nernst e gli effetti Hall classici e quantistici intorno alla temperatura ambiente basati sulle alte temperature di Curie dei composti di Heusler e dei loro parenti hanno il potenziale per avere un grande impatto nella conversione dell'energia e nei dispositivi elettronici quantistici per la spintronica o l'informatica quantistica.