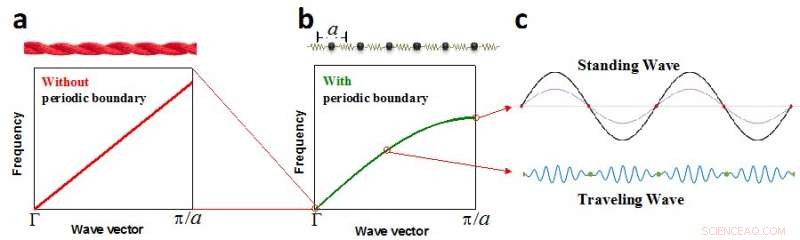
(a) dispersione fononica lineare basata sull'assunzione di onde elastiche acustiche, (b) dispersione fononica sinusoidale considerando la condizione periodica al contorno, (c) onda stazionaria reticolare (in alto) e onda viaggiante (in basso). Credito:Science China Press
La conduttività termica reticolare influenza fortemente le applicazioni dei materiali legate alla funzionalità termica, come la gestione termica, rivestimenti a barriera termica e termoelettrici. Al fine di comprendere la conducibilità termica del reticolo in modo più quantitativo e in modo efficiente in termini di tempo e costi, molti ricercatori hanno dedicato i loro sforzi e sviluppato alcuni modelli fisici usando dispersioni approssimate di fononi nel secolo scorso.
La maggior parte di questi modelli utilizza una dispersione fononica lineare, proposta da Debye nel 1912 sulla base di un presupposto acustico-elastico-onda (Fig. 1a), mentre altri modelli implicano parametri di adattamento sulla dispersione dei fononi o mancano di equazioni dettagliate per le proprietà di trasporto dei fononi. La dispersione fononica lineare di Debye offre molte semplificazioni sulle proprietà di trasporto fononico, ed era l'approssimazione più comune nel secolo scorso. La dispersione lineare di Debye prevede con successo la dipendenza T3 della capacità termica a temperature molto basse, e la capacità termica si avvicina al limite di Dulong-Petit alle alte temperature. Però, la natura della periodicità sulle disposizioni atomiche porta a una condizione al contorno periodica per le vibrazioni reticolari nei solidi (Fig. 1b), che in realtà crea onde stazionarie reticolari ai confini di Brillouin (Fig. 1c). Questo non soddisfa l'ipotesi dell'onda elastica-acustica di Debye, come proposto da Born e von Karman (BvK) nel 1912, lo stesso anno in cui Debye propose la dispersione lineare.
Ciò si traduce in una deviazione significativa della dispersione di Debye per i materiali cristallini periodici quando i fononi con vettori d'onda sono vicini ai confini di Brillouin (fononi ad alta frequenza). Quando questi fononi sono coinvolti per il trasporto fononico (cioè a temperature non estremamente basse), La dispersione di Debye porta a una sovrastima della conduttività termica del reticolo a causa della sovrastima della velocità di gruppo per questi fononi ad alta frequenza, come osservato in materiali con centinaia di conducibilità termica reticolare misurata nota e dettagli necessari per una previsione del modello conveniente in termini di tempo e costi secondo le nostre migliori conoscenze (Fig. 2g e h che mostrano una deviazione assoluta media di ~ + 40%). Inoltre, La dispersione di Debye sovrastima anche il limite inferiore teoricamente disponibile della conduttività termica del reticolo, portando le violazioni della conducibilità termica reticolare misurata ad essere addirittura inferiori all'attuale minimo teorico previsto (basato sul modello di Debye-Cahill) come osservato in decine di materiali.
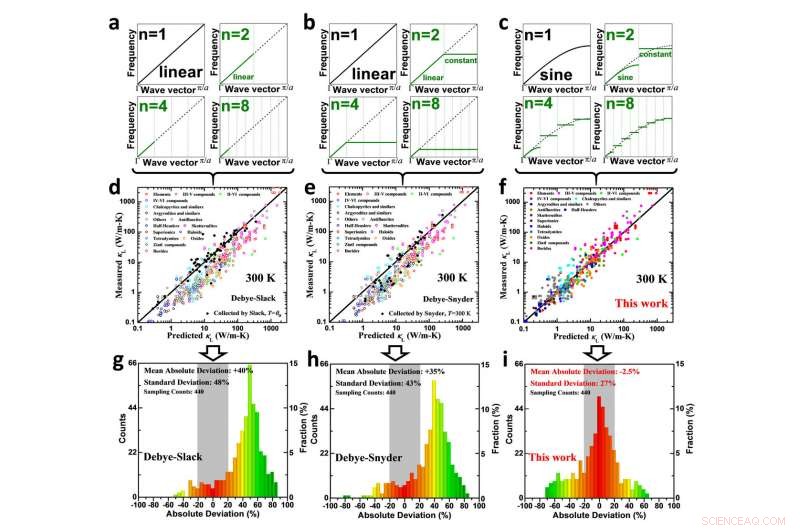
Confronto sulla dispersione fononica (a, b e c), conducibilità termica reticolare misurata rispetto alla previsione (d, e e f) e le corrispondenti analisi degli errori (g, h e i) per il modello Debye-Slack (a, d e g), Modello di Debye-Snyder (b, e e h) e quella sviluppata in questo lavoro considerando la condizione periodica al contorno (c, g e i) per i solidi cristallini. Credito:Science China Press
Questo lavoro tiene conto della condizione al contorno BvK, e rivela che il prodotto delle dispersioni acustiche e ottiche produce una funzione seno. Nel caso in cui il contrasto di massa (o la costante di forza) tra gli atomi sia grande, la dispersione acustica tende ad essere una funzione seno. Questa dispersione di tipo seno infatti esiste sia nei materiali più semplici che in quelli più complessi. Approssimando la dispersione acustica ad essere sinusoidale, la condizione al contorno BvK riduce successivamente i restanti rami ottici ad essere una serie di modi localizzati con una serie di frequenze costanti. Mentre i calcoli dei primi principi consentono una dispersione fononica più dettagliata, uno sviluppo della dispersione dei fononi razionalizzata per una previsione efficiente in termini di tempo e costi del trasporto di fononi è significativo a causa del dispendio di tempo e computazionalmente costoso per i calcoli dei primi principi.
Questo lavoro utilizza la suddetta razionalizzazione delle dispersioni fononiche, che consente di includere entrambi i contributi alla conduttività termica reticolare dei fononi acustici e ottici. Questo miglioramento nelle dispersioni di fononi migliora significativamente l'accuratezza di una previsione economica e temporale sulla conduttività termica reticolare dei solidi senza parametri di adattamento (Fig. 2c, mostrando una deviazione media assoluta di solo -2,5%), e quindi offre una progettazione più precisa dei solidi con conduttività termica reticolare prevista. Per di più, questo lavoro rimuove con successo la contraddizione della conducibilità termica del reticolo misurata che è addirittura inferiore al minimo teorico previsto sulla base di una dispersione lineare di Debye (Fig. 3). Ciò fornirebbe la possibilità teorica di razionalizzare la conducibilità termica del reticolo per essere inferiore a quanto attualmente si pensa, aprendo ulteriori opportunità per l'avanzamento di materiali termicamente resistivi per applicazioni, compreso il termoelettrico.
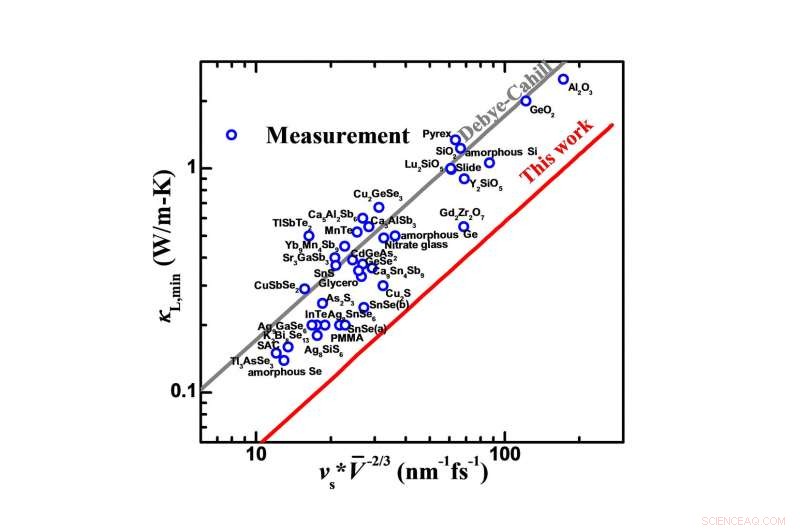
Confronto sulla conduttività termica minima del reticolo misurata (?L, min) e predizioni basate su una dispersione sviluppata secondo la condizione al contorno periodica o su una dispersione lineare di Debye (modello Debye-Cahill). Credito:Science China Press