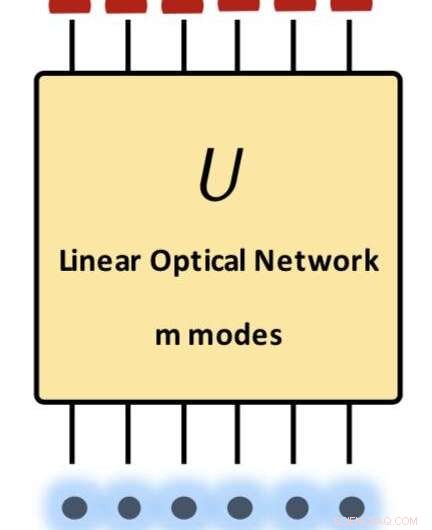
Riassunto del nostro risultato principale:un limite superiore delle ampiezze di transizione per l'ottica lineare. Gli stati iniziale e finale sono prodotti degli stati di Fock. La matrice U presenta qualsiasi trasformazione unitaria realizzabile in ottica lineare. Credito:Science China Press
L'ottica lineare costituisce uno dei migliori esempi di dimostrazione della fisica quantistica. Funziona a temperatura ambiente, e può essere osservato con dispositivi relativamente semplici. L'ottica lineare coinvolge processi fisici che conservano il numero totale di fotoni. Nel caso ideale, se ci sono 100 fotoni all'inizio, non importa quanto complicato sia il processo fisico, alla fine rimarranno esattamente 100 fotoni.
I fotoni sono particelle bosoniche non interagenti. Però, possono ancora interferire tra loro, esibendo effetti quantistici non banali. Un tipico esempio è l'esperimento Hong-Ou-Mandel, dove due fotoni identici vengono inviati a un dispositivo sperimentale. Dopo una semplice trasformazione lineare, i due fotoni appaiono come se fossero attaccati insieme e non volessero separarsi. Oltre a fornire una comprensione fondamentale della meccanica quantistica, lo studio dell'ottica lineare ha portato anche a molte applicazioni scientifiche.
Negli ultimi anni, le proprietà uniche dei sistemi ottici lineari hanno anche ispirato lo sviluppo della teoria della complessità computazionale. Nel 2012, Il professor Scott Aaronson al MIT (attualmente all'Università del Texas ad Austin) ha proposto un metodo ottico lineare per dimostrare la supremazia quantistica (computazionale), che si basa sul concetto di campionamento bosonico. Più specificamente, Aaronson ha suggerito che per una classe di problemi di campionamento basati su sistemi ottici lineari, sarebbe impossibile in pratica applicare qualsiasi computer classico per simulare. Questa idea scatena immediatamente una corsa per raggiungere lo status di "supremazia quantistica". Molti laboratori ottici quantistici in tutto il mondo si sono interessati allo sviluppo di sistemi di campionamento dei bosoni per battere i record in termini di numero di fotoni. D'altra parte, gli scienziati informatici sono impegnati nell'applicazione di supercomputer per alzare l'asticella per raggiungere la supremazia quantistica.
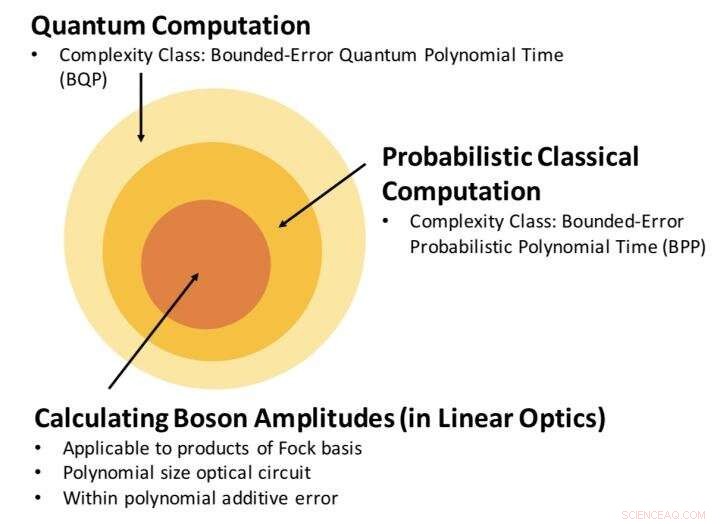
Relazione tra la classe di complessità della stima dell'ampiezza del bosone, e computazione classica e quantistica. Il nostro risultato stabilisce che calcolando l'ampiezza del bosone, con un errore polinomiale additivo, è un problema all'interno di BPP. Credito:Science China Press
Però, in termini di problemi pratici, l'applicazione del modello del campionamento bosonico non è un buon approccio. Perciò, Aaronson ha sollevato una domanda nel 2012:a parte i problemi di campionamento, i ricercatori possono sfruttare l'ottica lineare per raggiungere la supremazia quantistica in termini di problemi decisionali con una risposta SI/NO? Recentemente, Prof. Man-Hong Yung, professore associato di SUSTech e i suoi colleghi hanno pubblicato un articolo intitolato "Universal bound on sampling bosons in linear optics and its computational implicazioni" in Rassegna scientifica nazionale ( NSR ), offrendo una soluzione completa al problema aperto posto da Aaronson.
Nello specifico, Il team di Yung ha scoperto un limite fondamentale alle probabilità di transizione dei sistemi ottici lineari, limitare la capacità di trasferire bosoni utilizzando dispositivi ottici lineari. Insieme agli strumenti dell'ottica quantistica, hanno sviluppato un algoritmo classico in grado di stimare in modo efficiente l'ampiezza della transizione con un errore limitato. Di conseguenza, questi risultati portano a una risposta negativa al problema aperto di Aaronson. In altre parole, per la codifica di problemi di decisione difficile, è necessario utilizzare sistemi di ottica quantistica più complicati invece della sola ottica lineare.
Come dominio interdisciplinare tra fisica quantistica e informatica, la scienza dell'informazione quantistica resta un'area di ricerca molto attiva. Da una parte, i risultati del team di Yung contribuiscono alla fondazione teorica dell'ottica quantistica; d'altra parte, oltre al campionamento del bosone, questi risultati indicano una nuova prospettiva sui problemi di complessità computazionale in termini di ottica quantistica. indubbiamente, nel futuro, dovremmo aspettarci di vedere molti altri risultati entusiasmanti come questi in questo settore.