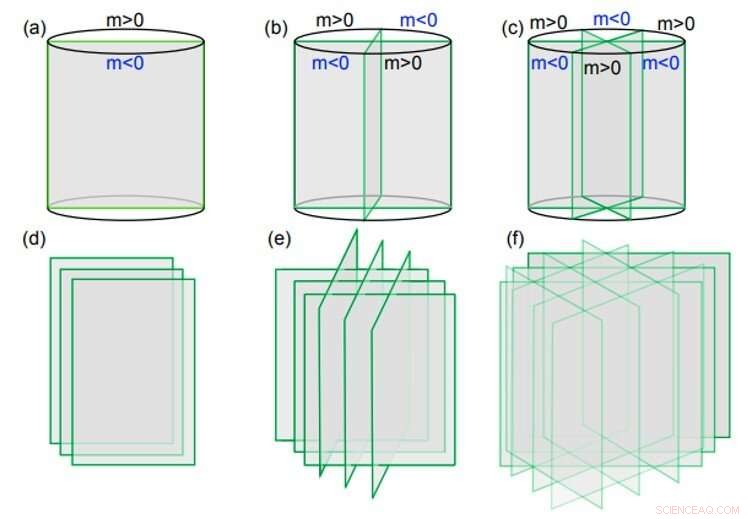
Costruzioni nello spazio reale per C2, 4, Simmetrie a 6 rotazioni e inversione temporale. (a-c) mostrano in assenza di simmetrie di traslazione, le costruzioni minime del duplice, stati topologici protetti da simmetria di rotazione quadrupla e sesta in tre dimensioni, dove ogni piano è uno stato topologico protetto da simmetria interna bidimensionale di bosoni o fermioni. Se è un isolante topologico bidimensionale, gli stati risultanti sono gli isolanti cristallini topologici studiati nel testo. (d-f) sono semplici estensioni delle costruzioni minime, costruzione di modelli tridimensionali con simmetrie di traslazione. Credito:progressi scientifici, doi:10.1126/sciadv.aat2374.
In un nuovo rapporto su Progressi scientifici , Chen Fang e Liang Fu del Laboratorio Nazionale di Pechino per la Fisica della Materia Condensata in Cina, Istituto Kavli per le scienze teoriche e il Dipartimento di Fisica, Massachusetts Institute of Technology negli Stati Uniti Scoperta dettagliata di nuovi tipi di anomalie quantistiche in sistemi bidimensionali con simmetria di inversione temporale (T) (conservazione dell'entropia) e simmetria di rotazione discreta; dove una forma mantiene la stessa struttura dopo una rotazione parziale e un ordine. Hanno quindi realizzato fisicamente stati anomali sulla superficie di nuove classi di isolanti topologici cristallini (TCI) normali all'asse di rotazione e che supportano una modalità elicoidale. La presenza di modalità elicoidali ha permesso loro di formare un nuovo dispositivo quantistico da un isolante cristallino topologico noto come nanobarra elicoidale con conduttanza longitudinale quantizzata.
Un singolo tipo di fermione relativistico senza massa (particelle elementari) può avere anomalie quantistiche in cui la conservazione della corrente di simmetria globale è interrotta a livello quantistico. Esempi ben noti includono l'anomalia chirale dei fermioni di Weyl in tre dimensioni (3-D), e anomalia di parità in 2-D. Nel presente lavoro, Fang e Fu hanno presentato una nuova anomalia quantistica associata all'inversione temporale (T) e alla simmetria rotazionale discreta (C n =2, 4, 6). Tali anomalie potrebbero esistere solo nelle teorie che hanno rotto le simmetrie di rotazione continua in 2-D. Materiali specifici come i TCI (isolanti cristallini topologici) possono ospitare stati di superficie robusti che hanno una dispersione Dirac (simile al grafene) rispetto ai portatori senza massa. La rottura della simmetria protettiva all'interno di tali materiali può far sì che i vettori acquisiscano massa.
Formazione di nuove classi di TCI
Nei TCI, topologia e simmetria cristallina si intrecciano per formare stati superficiali con caratteristiche distinte. La rottura della simmetria dei cristalli nei TCI può conferire massa ai fermioni di Dirac privi di massa; perciò, la presenza di stati superficiali topologici protetti da simmetrie cristalline è una proprietà distintiva dei TCI. I 230 gruppi spaziali precedentemente identificati che descrivono tutte le possibili simmetrie cristalline consentono molte diverse classi di TCI. I ricercatori avevano precedentemente trovato una classe di TCI protetta da simmetria di riflessione nei semiconduttori IV-VI e un'altra classe di TCI protetta congiuntamente da riflessione di scorrimento e simmetria di inversione del tempo all'interno di isolanti a grande distanza per formare fermioni sperimentali a "clessidra", mentre teorizzava diverse altre classi di TCI.

Gli schemi degli stati gapless in due dimensioni che hanno simmetrie di rotazione e inversione temporale. Ci sono (A) due, (B) quattro, e (C) sei coni di Dirac, legati l'uno all'altro da due, quattro-, e sei volte simmetrie di rotazione, rispettivamente, nella prima zona di Brillouin. I contorni sono i confini delle zone invarianti di Brillouin, lungo il quale la fase Berry viene quantizzata a zero o π.Credit:Science Advances, doi:10.1126/sciadv.aat2374.
La procedura di ricerca standard per trovare materiali topologici prevede il calcolo della struttura a bande di un particolare materiale per comprendere gli stati elettronici, quindi inserisci queste informazioni in una formula per rivelare se il materiale è topologico. Inoltre, la struttura a banda elettronica, nota come relazione tra l'energia di un elettrone e il suo quasi-impulso, può determinare se un materiale è un metallo o un isolante. I ricercatori hanno recentemente dimostrato una teoria per prevedere e scoprire sperimentalmente tali materiali topologici. Nel presente lavoro, perciò, Fanta et al. ha previsto una nuova classe di TCI protetti congiuntamente da rotazione n volte e simmetria di inversione temporale per mostrare stati superficiali topologici contenenti coni Dirac senza massa sulle superfici superiore e inferiore.
Comprensione dell'anomalia di rotazione
Lo studio dell'anomalia li ha portati a teorizzare nuove classi di invarianti di inversione temporale (dove le leggi sottostanti non sono sensibili alla direzione del tempo) TCI con C n =2, 4, 6 simmetria di rotazione. Questi TCI presentavano stati superficiali anomali sulle superfici superiore e inferiore. Per ogni nuova classe di TCI, il team ha costruito l'invariante topologico corrispondente relativo alle funzioni d'onda di Bloch nello spazio del momento. Basato sulla riduzione dimensionale (numero di variabili casuali o attributi in esame) e sugli stati della parete del dominio (strutture magnetiche di larghezza finita che separano regioni di magnetizzazione uniforme all'interno di un materiale magnetico), gli scienziati hanno inoltre fornito una comprensione unificata dello spazio reale di questi TCI. Hanno previsto diversi materiali per realizzare gli stati superficiali anomali protetti da simmetrie di rotazione doppie e quadruple. I ricercatori hanno quindi proposto un nuovo dispositivo quantistico basato sulle anomalie, noto come "asta elicoidale, " realizzato utilizzando questi nuovi TCI.
Due distinte strutture pseudospin che conservano C2. La struttura di pseudospin lungo un contorno di uguale energia per alcuni E> 0, nelle Hamiltoniane efficaci (A) h+(kx, ky) =kxσx + kyσy e (B) h−(kx, ky) =kxσx − kyσy. Si vede che la struttura di sinistra ha simmetria di rotazione continua e quella di destra no; si vede anche che la struttura di destra conserva ancora la duplice rotazione. Credito:progressi scientifici, doi:10.1126/sciadv.aat2374. 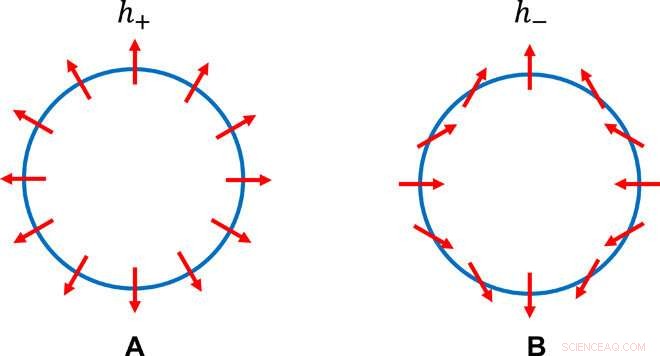
Per costruire i nuovi TCI e formare la topologia nello spazio del momento, Fanta et al. potrebbe aggiungere due invarianti di inversione temporale (simmetria T), forti isolanti topologici (TI) ciascuno con simmetria rotazionale n volte. Hanno considerato l'ibridazione consentita dalla simmetria tra i fermioni di Dirac di superficie ai TI per ottenere gli stati superficiali desiderati dei TCI. I ricercatori hanno descritto i fermioni di Dirac usando h + e h - trame di spin simili a vortici nello spazio del momento con chiralità destrorsa e sinistra. I ricercatori hanno osservato la presenza e l'assenza di simmetria di rotazione continua osservando il modello del vettore pseudospin su alcuni contorni di uguale energia di h + e h - rispettivamente.
Dopo aver stabilito la struttura a bande dello stato superficiale del TI, Fanta et al. fornito una spiegazione alternativa della loro natura topologica dal punto di vista dello spazio reale, simile a un approccio di ricerca precedente. L'approccio dello spazio reale ha aggiunto perturbazioni consentite dalla simmetria per rompere la simmetria traslazionale e creare un gap tra i fermioni di Dirac privi di massa sulla superficie per ulteriori studi. I fenomeni hanno facilitato stati TCI non banali e dimostrazioni della loro robustezza sotto interazioni elettroniche. Per questo, hanno considerato un modello a doppio TI di un TCI posto all'interno di un cilindro di dimensioni maggiori della lunghezza di correlazione e della superficie, liscio su scala atomica. Per C 4, 6 -TCI posto su un cilindro, le posizioni dei modi sugli stati superficiali non erano fissate a nessun cardine fisico o intersezione di superfici cristalline. Sebbene la forma cilindrica contenesse una simmetria di rotazione continua, il sistema descritto nello studio lo ha scomposto in simmetria rotazionale discreta, per indicare l'esistenza di linee 1-D gapless anche su un cilindro liscio perfettamente atomico.
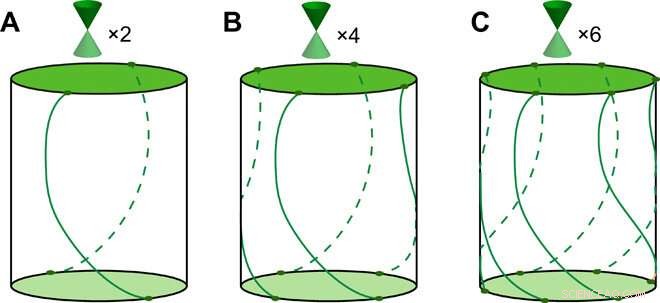
Stati superficiali di rotazione TCI. Schemi degli stati superficiali sulle superfici superiore e inferiore e degli stati marginali sulle superfici laterali altrimenti aperte dei nuovi TCI protetti da (A) duplice, (B) quadruplo, e (C) simmetrie di rotazione sei volte nella geometria dell'asta. Le superfici superiore e inferiore hanno coni di Dirac, e sulla superficie laterale, Due, quattro, e sei modalità di bordo elicoidale collegano le due superfici; possono avere forma e posizione arbitrarie ma sono collegati tra loro da due, quattro-, e sei rotazioni, rispettivamente. Credito:progressi scientifici, doi:10.1126/sciadv.aat2374.
Fanta et al. ha poi rilevato la possibilità di comprendere gli stati cristallini topologici da una prospettiva di riduzione dimensionale, dove lo stato 3-D potrebbe essere considerato come un insieme di strati disaccoppiati di stati topologici 2-D. Tutti e tre i tipi di nuovi TCI introdotti in questo lavoro potrebbero quindi essere costruiti da TI 2-D. Fanta et al. hanno usato questa costruzione per estendere la loro teoria degli stati topologici protetti dalla simmetria fortemente interagenti protetti dalla simmetria di rotazione e da qualsiasi simmetria locale tra cui, ma non limitato alla simmetria di inversione temporale.
Poiché è noto che i modi elicoidali 1-D sono privi di back-scatter a causa della simmetria di inversione temporale, questa proprietà unica ha permesso a Fang et al. per progettare un nanorod elicoidale da questi nuovi materiali. Ogni modalità elicoidale richiedeva solo una simmetria di inversione temporale per la protezione e la simmetria di rotazione assicurava che le modalità n-elicoidali non si incrociassero nello spazio reale e si staccassero. In questo modo, fintanto che la simmetria di rotazione non era considerevolmente rotta, queste modalità del bordo elicoidale rimarrebbero stabili, sebbene non siano più correlati tra loro tramite una rotazione, per formare nuove classi di TCI con anomalia di rotazione della superficie.
© 2020 Scienza X Rete