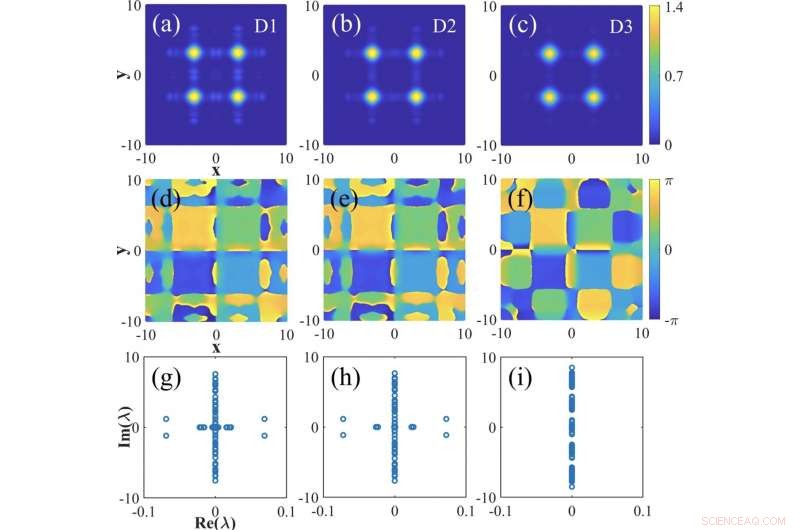
Trame di contorno, fasi, e autovalori di solitoni con gap di vortice che appaiono come stati legati a modalità quadrupla. Credito:XIOPM
I solitoni sono oggetti stabili bilanciati da diffrazione o dispersione e non linearità. Una sfida fondamentale in questo campo è la stabilizzazione dei solitoni in coordinate multidimensionali, poiché i solitoni 2-D e 3-D nello spazio libero sono sempre instabili e subiscono rispettivamente collassi critici derivanti da catastrofiche non linearità autofocalizzanti.
La stabilizzazione di stati localizzati multidimensionali di solito si basa su mezzi periodici lineari con non linearità uniforme. Sebbene i reticoli non lineari con variazione regolare della non linearità possano supportare varie specie di solitoni. Però, L'esistenza e la proprietà di stabilità dei solitoni con non linearità cubico-quintiche e potenziale periodico lineare 2-D devono ancora essere rivelate. Esistono alcuni modelli o metodi per prevenire il collasso critico dei solitoni di ordine superiore?
Un gruppo di ricerca guidato dal Prof. Dr. Zeng Jianhua dell'Istituto di ottica e meccanica di precisione di Xi'an (XIOPM) dell'Accademia cinese delle scienze (CAS) propone uno schema fattibile per stabilizzare le modalità localizzate 2-D contro il collasso critico considerando il ordine di diffrazione frazionaria alla propagazione della luce in sistemi fisici periodici con non linearità autofocalizzanti e autodefocalizzanti in competizione in termini non lineari cubico-quantici. Il risultato è stato pubblicato in Fisica delle comunicazioni .
Propongono teoricamente una struttura dell'equazione di Schrödinger frazionaria non lineare 2-D (NLFSE), che può sopprimere il crollo critico. Rivelano che il modello produce una varietà di famiglie di solitoni stabili, inclusi gap fondamentale 2-D e solitoni verticali e cluster solitoni gap (i solitoni sono sempre instabili nel modello solo quintico).
Un'analisi dettagliata delle proprietà dinamiche dei solitoni mostra inoltre che i solitoni sono robustamente stabili nel mezzo delle lacune di banda del sottostante spettro lineare di Bloch, mentre instabile vicino ai bordi dei band gap; e la stabilità dei solitoni è moderatamente influenzata dalla forza non lineare.
La notevole scoperta offre una nuova strada per studiare l'esistenza e le proprietà dinamiche dei modi localizzati 2-D gestendo l'ordine di diffrazione e le lacune di banda sintonizzabili dei sistemi fisici periodici.