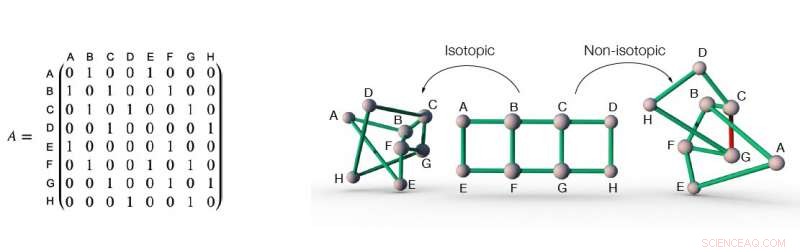
La matrice di adiacenza di una rete (a sinistra), e tre diversi inserimenti di questa rete nello spazio (a destra). La matrice di adiacenza di una rete registra le informazioni sulla connettività della rete. Per esempio, nella rete in figura, i nodi A e B sono collegati da un collegamento, quindi l'elemento nella matrice di adiacenza all'intersezione della riga A e della colonna B è uno. Allo stesso modo, i nodi A e C non sono collegati da un collegamento, quindi l'elemento nella matrice di adiacenza all'intersezione della riga A e della colonna C è zero. I primi due incorporamenti di rete della rete descritta dalla matrice di adiacenza a sinistra sono isotopici l'uno rispetto all'altro, perché possono essere trasformati l'uno nell'altro semplicemente "appiattindo" l'incastonatura, senza la necessità di tagliare alcun collegamento aperto. D'altra parte, l'immersione a destra non è isotopica rispetto alle altre due immersioni, perché per trasformarlo negli altri due, almeno un collegamento (ad esempio il collegamento rosso) deve essere aperto per consentire il passaggio di altri collegamenti. Credito:Liu, Dehmamy &Barabasi.
La struttura e le funzioni di molte reti fisiche, compreso il cervello umano, il sistema vascolare e altre reti biologiche, spesso dipendono dalla loro disposizione tridimensionale e geometrica. Distinguere tra reti fisiche con connessioni identiche ma layout geometrici diversi, però, può essere molto impegnativo.
I ricercatori della Northeastern University hanno recentemente introdotto un costrutto teorico chiamato isotopia di rete che potrebbe aiutare gli scienziati a distinguere tra reti fisiche. L'isotopia di rete offre uno strumento di classificazione che delinea classi di layout di rete 3D che possono essere trasformati l'uno nell'altro senza incroci di collegamento.
"Il nostro progetto nasce come curiosità sui layout di rete, "Yanchen Liu, uno dei ricercatori che ha condotto lo studio, ha detto a Phys.org. "Nel nostro ufficio ci sono molte reti stampate in 3D che sono state studiate in vari progetti in laboratorio. Osservando queste reti, ci siamo chiesti:se per una data rete (cablaggio fisso dei collegamenti) esistono infiniti modi per posizionare i nodi e i collegamenti nello spazio 3D, come possiamo sapere se due layout della stessa rete sono uguali o diversi? Inoltre, come dovremmo definire le somiglianze tra i layout di rete e se due layout sono diversi, come dovremmo misurare il livello di differenza tra loro?"
Poco dopo aver iniziato a condurre le loro ricerche, Liu ei suoi colleghi si sono resi conto che ci sono due modi principali in cui i layout geometrici della rete possono differire l'uno dall'altro. Il primo di questi dipende dalla misura in cui è allungato il layout di una rete, mentre il secondo risulta dal cosiddetto link-crossing (cioè, collegamenti che si incrociano).
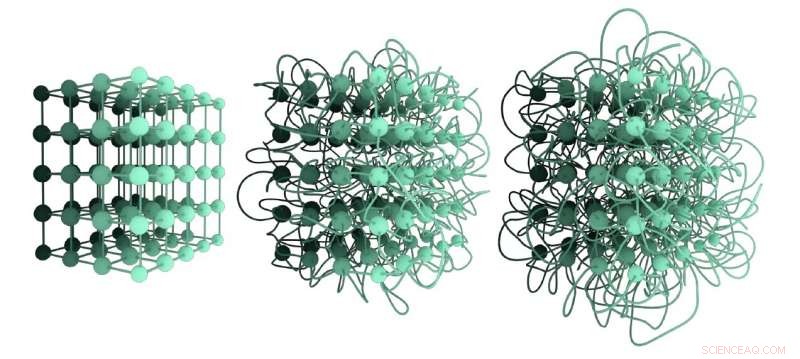
Tre diversi immergimenti non isotopici della stessa rete reticolare. L'incastonatura a sinistra è districata; l'incasso al centro è più intricato rispetto al primo, e il terzo incastonatura è il più intricato. Il loro livello di aggrovigliamento può essere quantificato dal Graph Linking Number. Credito:Liu, Dehmamy &Barabasi.
"Il primo tipo di differenza è banale, ma il secondo tipo di differenza è intrigante, " ha spiegato Liu. "Domande simili sono state studiate nella teoria dei nodi, che è un campo dedicato ai nodi formati da una o più curve chiuse."
L'incorporamento di una rete fisica (ovvero, layout) è essenzialmente una descrizione di come i suoi nodi e collegamenti sono messi insieme nello spazio. Nella loro carta, Liu e i suoi colleghi hanno introdotto un concetto chiamato isotopia di inclusione di rete che può essere utilizzata per distinguere tra diversi possibili inserimenti di una determinata rete nello spazio 3D.
"Se due incorporamenti di rete sono isotopici l'uno rispetto all'altro, significa che possono essere allungati l'uno nell'altro senza dover tagliare alcun collegamento aperto per far passare altri collegamenti, " Liu ha detto. "D'altra parte, se due incorporamenti di rete non sono isotopici l'uno rispetto all'altro, significa che non possono mai essere trasformati continuamente l'uno nell'altro senza tagliare i collegamenti".
La nozione di isotopia di rete, come è definito da questo team di ricercatori, può essere utilizzato per misurare la misura in cui i diversi incorporamenti di rete sono aggrovigliati, una misura denominata numero di collegamento del grafico. interessante, Liu e i suoi colleghi hanno scoperto che questa misura è anche correlata all'energia elastica di un layout.
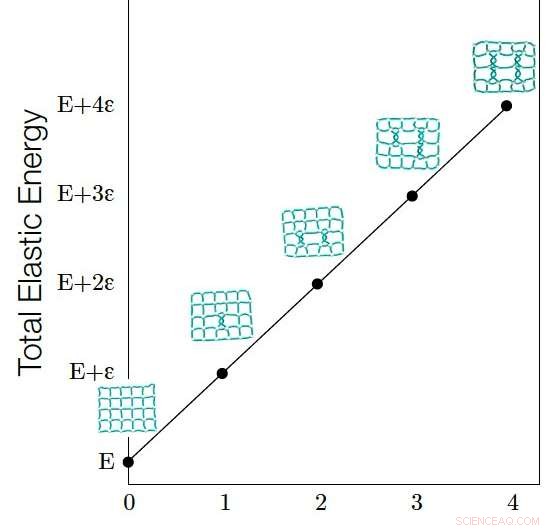
Si osserva che l'energia elastica (E) di un'immersione in una rete è linearmente correlata al suo Graph Linking Number (G). L'energia elastica di un'immersione in una rete è proporzionale alla lunghezza totale di tutti i collegamenti. La relazione lineare tra E e G può essere spiegata dal fatto che ogni aumento di G allunga i collegamenti nell'immersione della rete, che a sua volta aumenta E, e la quantità di aumento di energia causata da ogni groviglio (ogni groviglio fa sì che G aumenti di uno) è quantizzata e una costante. Credito:Liu, Dehmamy &Barabasi.
Molti sistemi fisici possono essere descritti come reti, una parte significativa delle quali sono reti fisiche. I concetti teorici introdotti dai ricercatori sono strumenti efficaci per studiare le proprietà e le caratteristiche geometriche di questi sistemi.
"Ci sono tre importanti risultati in questo documento, secondo me, " Liu ha detto. "Il primo è che abbiamo definito l'isotopia dell'incorporamento di rete, che è un'estensione dell'isotopia dei nodi dalla teoria dei nodi agli incorporamenti di rete. Il secondo è che abbiamo inventato il numero di collegamento del grafico, un'utile misura del livello di aggrovigliamento degli embedding di rete. Finalmente, abbiamo scoperto che il numero di collegamento del grafico di un'incorporazione di rete è correlato con l'energia elastica di quell'incorporamento di rete".
Liu e i suoi colleghi hanno utilizzato le loro scoperte per sviluppare un modello statistico che descrive la formazione di grovigli in una rete fisica. Nel futuro, questo modello potrebbe essere utilizzato per valutare la misura in cui il layout 3D di un sistema fisico è ingarbugliato.
Nel loro recente articolo, ad esempio, i ricercatori lo hanno usato per esaminare l'intreccio di molti sistemi fisici, compreso il cervello di topo. Poiché tutti i costrutti teorici introdotti in questo articolo possono essere applicati a un'ampia varietà di reti fisiche, potrebbero infine sostenere la ricerca in fisica concentrandosi su un'ampia gamma di argomenti.
"Stiamo continuando lo studio delle reti fisiche, " Liu ha detto. "Attualmente, Sto lavorando su una rete fisica specifica:la rete cerebrale larvale del moscerino della frutta, che è una rete formata da neuroni incorporati nello spazio 3D. Siamo particolarmente interessati alle connessioni tra la fisicità di questa rete (il suo inserimento) e le sue proprietà strutturali (come i neuroni sono collegati attraverso i cablaggi neuronali)."
© 2020 Scienza X Rete