
Credito:CC0 Dominio Pubblico
Negli ultimi anni, calcolo del serbatoio fisico, una delle nuove tecnologie di elaborazione delle informazioni, ha attirato molta attenzione. Questa è una versione di implementazione fisica del calcolo del serbatoio, che è un metodo di apprendimento derivato dalla teoria delle reti neurali ricorrenti (RNN). Implementa il calcolo considerando il sistema fisico come un enorme RNN, esternalizzando le principali operazioni alla dinamica del sistema fisico che costituisce il serbatoio fisico. Ha il vantaggio di ottenere l'ottimizzazione istantaneamente con risorse computazionali limitate regolando le ponderazioni di lettura lineari e statiche tra l'uscita e un serbatoio fisico senza richiedere l'ottimizzazione delle ponderazioni mediante propagazione all'indietro.
Però, poiché la capacità di elaborazione delle informazioni dipende dalla capacità fisica del giacimento, è importante che questo sia studiato e ottimizzato. Per di più, quando si progetta un serbatoio fisico con un'elevata capacità di elaborazione delle informazioni, si prevede che il costo sperimentale sarà ridotto mediante simulazione numerica. Esempi ben noti di calcolo del serbatoio fisico includono la sua applicazione a materiali morbidi, fotonica, spintronica, e quanti, mentre negli ultimi anni, molta attenzione è stata dedicata alle onde; sono stati proposti dispositivi neuromorfici che simulano le funzioni del cervello utilizzando onde non lineari.
Il flusso fluido dell'acqua, aria, ecc. rappresenta un sistema fisico che è familiare ma mostra vari e complicati schemi che si pensava avessero un'elevata capacità di elaborazione delle informazioni. Però, Il calcolo del serbatoio fisico virtuale utilizzando la simulazione numerica o l'indagine sulla capacità di elaborazione delle informazioni dei fenomeni di flusso dei fluidi non è stato realizzato a causa del suo costo computazionale numerico relativamente elevato. Perciò, la relazione tra il vortice di flusso e la capacità di elaborazione delle informazioni è rimasta sconosciuta.
In questo studio, Il Prof. Hirofumi Notsu e uno studente laureato dell'Università di Kanazawa in collaborazione con il Prof. Kohei Nakajima dell'Università di Tokyo hanno studiato i fenomeni di flusso dei fluidi come un sistema fisico, soprattutto il flusso di fluido che si verifica attorno a un cilindro, che si comprende bene. È noto che questo sistema fisico è governato dalle equazioni incomprimibili di Navier-Stokes, che descrivono il flusso del fluido, e include anche il numero di Reynolds, un parametro indicativo delle caratteristiche del sistema.
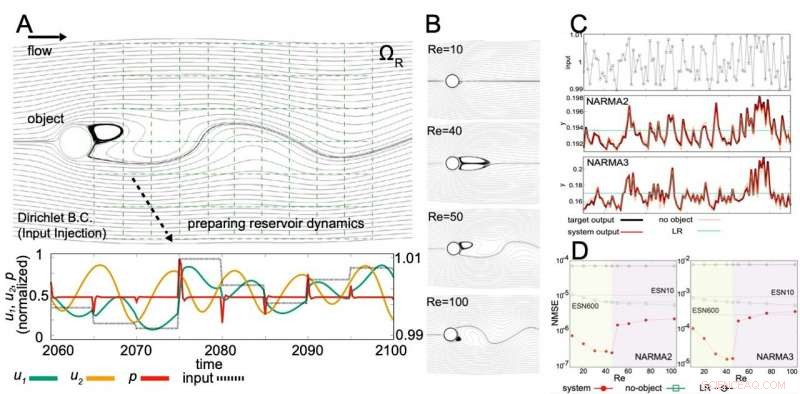
R:Schema dello studio. B:Flusso di fluido tipico ad ogni numero di Reynolds. C:Input lungo la sequenza temporale e risultati dei modelli NARMA2 e NARMA3. I valori target sono in nero mentre i valori del calcolo del serbatoio fisico virtuale utilizzando i vortici sono in rosso. D:Valori degli errori (errori quadratici medi normalizzati, NMSE) ad ogni numero di Reynolds nei modelli NARMA2 e NARMA3. L'errore è minimo con il numero di Reynolds intorno a 40. Credito:Kanazawa University
Questo sistema fisico è stato virtualmente implementato mediante simulazione numerica spaziale bidimensionale utilizzando il metodo stabilizzato di Lagrange-Galerkin, e la dinamica della velocità del flusso e della pressione nei punti selezionati nella regione a valle del cilindro è stata utilizzata come serbatoio fisico. La capacità di elaborazione delle informazioni è stata valutata utilizzando il modello NARMA.
È noto che nel flusso di fluido attorno a un cilindro, all'aumentare del valore del numero di Reynolds, i vortici gemelli formati nella regione a valle del cilindro diventano gradualmente più grandi e alla fine formano una strada vorticosa di Karman, lo spargimento alternato di vortici. In questo studio, è stato chiarito che al numero di Reynolds dove i vortici gemelli sono massimi ma appena prima del passaggio a una strada vorticosa di Karman, la capacità di elaborazione delle informazioni è la più alta.
In altre parole, prima del passaggio a una strada vorticosa di Karman, la capacità di elaborazione delle informazioni aumenta all'aumentare della dimensione dei vortici gemelli. D'altra parte, poiché la proprietà dello stato dell'eco che garantisce la riproducibilità del calcolo del serbatoio non può essere mantenuta quando avviene il passaggio alla strada del vortice di Karman, diventa chiaro che la strada del vortice di Karman non può essere utilizzata per l'informatica.
Si prevede che questi risultati relativi ai vortici del flusso di fluido e alla capacità di elaborazione delle informazioni saranno utili quando, in futuro, la capacità di elaborazione delle informazioni del giacimento fisico può essere ampliata utilizzando il flusso di fluido, per esempio. nello sviluppo di dispositivi neuromorfici basati su onde recentemente riportati. Sebbene il costo computazionale numerico dei fenomeni di flusso dei fluidi sia relativamente elevato, questo studio ha reso possibile gestire vortici macroscopici che sono fisicamente facili da capire e ha chiarito la relazione tra vortici e capacità di elaborazione delle informazioni implementando virtualmente il calcolo del serbatoio fisico con simulazione numerica spaziale bidimensionale.
Calcolo del serbatoio fisico virtuale, che veniva applicato a un numero relativamente elevato di sistemi fisici descritti come sistemi unidimensionali, è stato ampliato per includere sistemi fisici con due o più dimensioni spaziali. Si prevede che i risultati di questo studio consentiranno l'indagine virtuale delle capacità di elaborazione delle informazioni di una più ampia gamma di sistemi fisici. Inoltre, poiché è emerso che i vortici sono la chiave per la capacità di elaborazione delle informazioni, si prevede che sarà ulteriormente promossa la ricerca per la creazione o il mantenimento dei vortici.