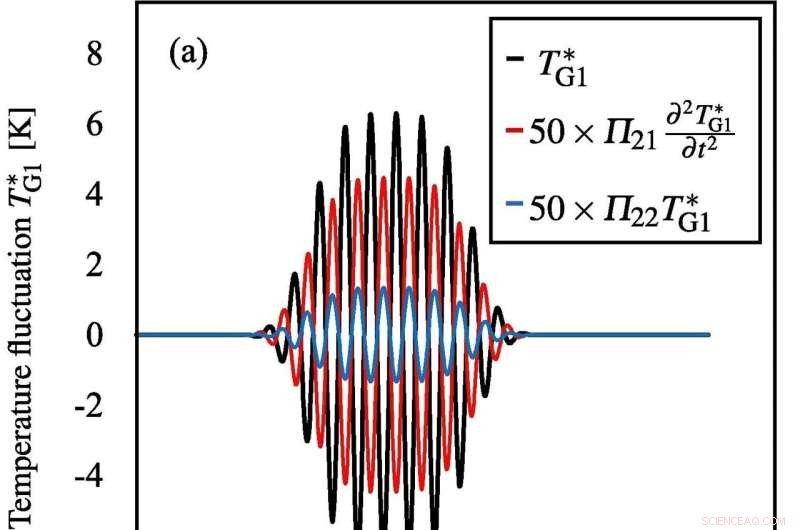
Andamento temporale della fluttuazione di temperatura TG1 ∗ (a) alla sorgente sonora (condizione al contorno) e (b) al fuoco della Fig. 3 (a), dove il gas all'interno della bolla è Argon. Le curve nera, rossa e blu rappresentano le forme d'onda della fluttuazione della temperatura, il termine di dissipazione dovuto alla viscosità interfacciale e alla comprimibilità del liquido e il termine di dissipazione dovuto alla conducibilità termica del gas. Credito:Sonochimica a ultrasuoni (2022). DOI:10.1016/j.ultsonch.2022.105911
Gli scienziati della Graduate School of Systems and Information Engineering dell'Università di Tsukuba hanno creato un modello teorico per descrivere il movimento delle onde ultrasoniche in presenza di bolle multiple. Questo lavoro può aiutare i medici nella progettazione di nuove applicazioni diagnostiche e terapeutiche della tecnologia a ultrasuoni.
Trattamenti medici a ultrasuoni mirati per l'ablazione di tumori o la rottura dei calcoli renali con la litotripsia ad onde d'urto possono offrire la possibilità di migliorare i risultati del paziente senza esposizione a radiazioni elettromagnetiche o di particelle. Tuttavia, questi metodi si basano sulla comprensione del modo in cui le onde ultrasoniche si muovono attraverso ambienti complessi, come i tessuti viventi. Ciò è particolarmente vero per la terapia di ablazione del tumore, che agisce dirigendo il calore creato dagli ultrasuoni per distruggere le cellule malate. Sono necessarie equazioni di propagazione delle onde più complete per garantire che queste modalità vengano implementate correttamente.
Ora, gli scienziati dell'Università di Tsukuba hanno esteso il modello convenzionale di propagazione delle onde sonore per includere più bolle. L'equazione di Khokhlov-Zabolotskaya-Kuznetsov (KZK) è stata precedentemente utilizzata come modello semplificato per la propagazione non lineare di ultrasuoni focalizzati in un liquido puro. Essere in grado di scrivere una singola equazione per modellare gli ultrasuoni non lineari, le oscillazioni delle bolle e le fluttuazioni della temperatura in modo coerente apre la strada ad applicazioni mediche potenziate dalle microbolle.
"Un modello matematico per applicazioni mediche che utilizzano le bolle dovrebbe descrivere la non linearità sia della propagazione degli ultrasuoni che dell'oscillazione delle bolle", afferma l'autore, il professor Tetsuya Kanagawa. Gli scienziati hanno utilizzato un metodo per combinare più scale di dimensioni calcolando le equazioni di base della media volumetrica per i liquidi frizzanti. Le equazioni risultanti avevano termini per effetti non lineari, dissipazione del suono, dispersione e focalizzazione. In particolare, il termine stesso di dissipazione dipendeva da tre fattori:viscosità interfacciale del liquido, comprimibilità del liquido e conducibilità termica del gas all'interno delle bolle.
"In futuri perfezionamenti, possiamo aggiungere estensioni teoriche dell'equazione KZK che incorporano gli effetti viscosi del liquido sfuso, l'elasticità dei tessuti corporei e il trasferimento di calore", afferma il professor Kanagawa. Una delle prime applicazioni è l'uso di microbolle come agenti di contrasto per migliorare la risoluzione delle immagini ecografiche. Tuttavia, possono anche essere estesi agli interventi che realizzano l'ablazione mirata dei tessuti. + Esplora ulteriormente