I ricercatori guidati dal Prof. Xiaoyong Hu dell’Università di Pechino, in Cina, sono interessati alla fotonica topologica. Hanno proposto un approccio interdisciplinare per studiare i sistemi topologici attraverso l'entropia dell'informazione (IE) nello spazio reale.
Il lavoro è pubblicato sulla rivista Frontiers of Optoelectronics .
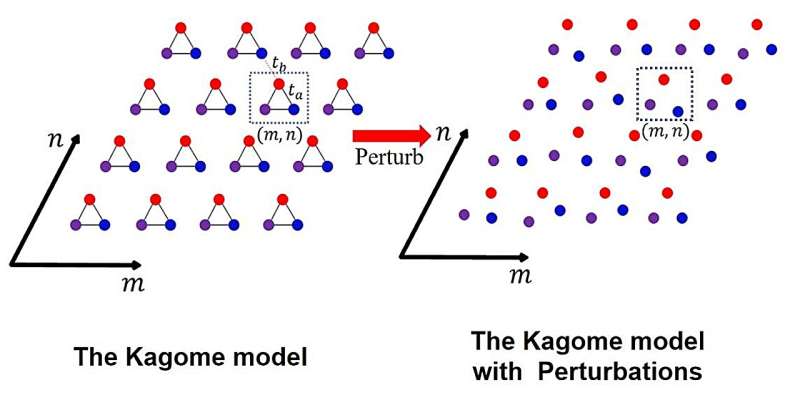
La fotonica topologica gioca un ruolo importante nei campi della fisica fondamentale e dei dispositivi fotonici. Il modello Kagome, il modello Su-Schrieffer-Heeger (SSH) e gli altri modelli topologici vengono utilizzati come piattaforma per studiare il nuovo fenomeno fisico e guida per progettare nuovi dispositivi fotonici come laser topologicamente protetti e robusti dispositivi di trasmissione.
Fino ad ora, i ricercatori hanno solitamente giudicato gli stati topologici in un cristallo fotonico sulla base di tre criteri:l'invariante topologico, incluso il numero di Chern, il numero di avvolgimento e Z2 invariante topologico; le distribuzioni o le lacune degli autovalori nella banda del cristallo fotonico; e le distribuzioni del campo elettrico degli stati topologici.
Quasi tutti i metodi precedenti si basano sulle strutture a bande negli spazi del momento. Tuttavia, è generalmente complicato analizzare le proprietà topologiche nello spazio della quantità di moto, soprattutto se sono presenti perturbazioni nel sistema. Le perturbazioni causeranno anche la chiusura del gap di banda del sistema topologico, il che renderà difficile analizzare la topologia nello spazio della quantità di moto.
Il modello di Kagome viene utilizzato come esempio di calcolo teorico e il processo di scomparsa dei suoi stati limite topologici (TES) viene osservato con IE. Il metodo IE può essere utilizzato per analizzare le distribuzioni modali dei TES e la transizione di fase topologica. Questo metodo può essere esteso anche al modello SSH e al cristallo fotonico Valley-Hall.
La ricerca fornisce un metodo per studiare la fase fotonica topologica basato sulla teoria dell'informazione e un'opportunità per analizzare le proprietà fisiche sfruttando l'interdisciplinarietà.
Ulteriori informazioni: Rui Ma et al, L'entropia dell'informazione ha consentito di identificare la fase fotonica topologica nello spazio reale, Frontiers of Optoelectronics (2024). DOI:10.1007/s12200-024-00113-7
Fornito dalla stampa per l'istruzione superiore