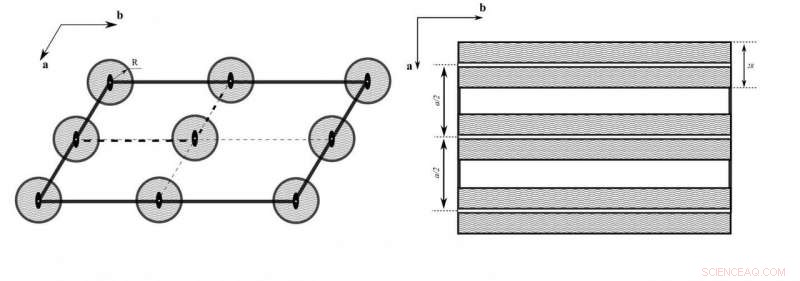
Volume proibito nei gruppi di simmetria spaziale bidimensionale:(sinistra) p2 e (destra) pm. Il riempimento ondulato indica le regioni vietate. Credito:Università Lobachevsky
È noto che la disposizione reciproca degli atomi nello spazio cristallino corrisponde al minimo dell'energia potenziale di interazione di tutti gli atomi cristallini. Il principio dell'energia potenziale minima può essere implementato in diversi modi geometrici per la descrizione approssimativa della disposizione atomica nei cristalli. In particolare, questi includono il principio dell'impaccamento ravvicinato per i cristalli di composti inorganici con legami non diretti e il principio dell'impaccamento ravvicinato delle molecole per i cristalli molecolari. I ricercatori del Dipartimento di Cristallografia e Fisica Sperimentale dell'Università Lobachevsky ritengono che quando si analizza la possibilità di implementare uno specifico gruppo spaziale come gruppo di simmetria cristallina, è importante considerare i fattori principali il volume e la forma della parte di spazio cristallino dove possono essere localizzati ioni o molecole, così come la simmetria delle molecole (a causa della presenza di sistemi regolari di punti in cui possono essere localizzati gli atomi di una data molecola).
"Se si considerano gli atomi come oggetti geometrici, che hanno un volume finito paragonabile al volume di una cella unitaria di cristallo, è necessario considerare le limitazioni geometriche sulla disposizione reciproca degli atomi nello spazio cristallino. Queste limitazioni sono dovute al fatto che la distanza tra due atomi non può essere inferiore alla somma dei loro raggi cristallochimici, ", afferma il professore dell'Università Lobachevsky Evgeny Chuprunov.
Ciascuno dei 230 gruppi spaziali di simmetria è caratterizzato da limitazioni specifiche sulla disposizione atomica nello spazio cristallino, che sono determinati dall'insieme degli elementi di simmetria dei gruppi spaziali, così come le dimensioni delle celle unitarie. Ciò significa che alcuni sistemi regolari di punti di questi gruppi non possono esistere in natura per ragioni puramente geometriche. L'insieme di questi punti forma "regioni proibite" nello spazio cristallino, e l'esistenza di tali regioni fu dimostrata dall'eccezionale chimico e cristallografo, vincitore del Premio Chugaev Mikhail Porai-Koshits.
"Abbiamo determinato la simmetria delle regioni proibite per l'imballaggio di cerchi solidi in uno spazio bidimensionale, la cui simmetria è descritta da uno dei gruppi di simmetria spaziale bidimensionale. È stato inoltre stabilito che, a seconda della simmetria delle regioni proibite, i gruppi di simmetria spaziale bidimensionale possono essere suddivisi in sette classi, "dice Nikolai Somov, professore associato del Dipartimento di Cristallografia e Fisica Sperimentale dell'UNN.
La simmetria delle regioni proibite è stata determinata dai ricercatori dell'Università Lobachevsky per l'imballaggio di sfere solide nello spazio cristallino tridimensionale di diversa simmetria. Secondo i risultati ottenuti, 230 gruppi di simmetria spaziale sono caratterizzati da 33 classi di simmetria spaziale di regioni proibite.
"L'approccio qui proposto può essere generalizzato per il caso di spazi n-dimensionali di dimensione maggiore e impacchettamento di elementi di forma più complessa, " riassume Evgeny Chuprunov.