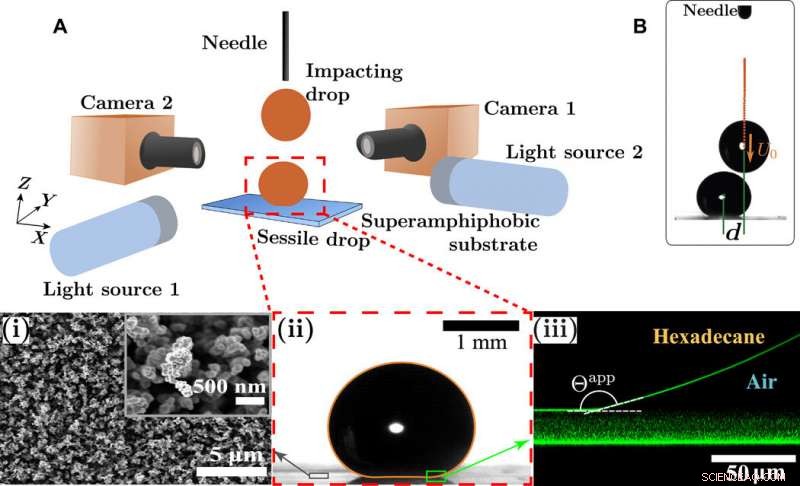
Approccio sperimentale e caduta sessile. (A) Schizzo della configurazione sperimentale per l'impatto della caduta binaria su superfici superanfifobiche. L'ago è fissato per impostare l'altezza d'urto in direzione Z e la distanza relativa tra le gocce sessili e d'urto. La caduta sessile viene prima centrata lungo il piano YZ. Quindi, la goccia impattante viene erogata dall'ago mentre l'impatto viene monitorato con la telecamera 2. La telecamera 1 viene utilizzata per determinare le posizioni relative delle gocce in direzione X. Le telecamere e le sorgenti luminose sono allineate per osservare l'impatto sia nei piani XZ che YZ. Riquadri:(i) Immagine SEM di una superficie sagomata con fuliggine a due ingrandimenti. (ii) Goccia di esadecano (V ≈ 3 μl) appoggiata sulla superficie superfifobica. Il contorno arancione è la soluzione dell'Eq. 1 per un corrispondente numero di Bond Bo =0,3. (iii) Immagine confocale che mostra una goccia di esadecano sulla superficie superfifobica. L'immagine illustra l'angolo di contatto apparente della goccia con la superficie (Θapp 164°). L'immagine viene scattata in modalità riflesso, cioè., nessun colorante è stato aggiunto all'esadecano. La riflessione della luce risulta dalle differenze tra gli indici di rifrazione dell'esadecano (1,43), aria (1.0), e vetro e silice (~1,46). Lo strato superfifobico è costituito principalmente da aria, e quindi, il suo indice di rifrazione è vicino a 1. Pertanto, sono visibili lo strato orizzontale vetro-superanfifobico e le interfacce strato esadecano-superanfifobico. Lo stesso strato superfifobico è visibile come un pattern diffuso, risultante dalla riflessione della luce dalle nanoparticelle di silice. (B) Immagine che mostra una collisione fuori centro. Il parametro di impatto è χ =d/(2R). Credito fotografico:Olinka Ramírez-Soto, Istituto Max Planck per la ricerca sui polimeri. Credito:progressi scientifici, doi:10.1126/sciadv.aba4330
Le goccioline che si scontrano sono onnipresenti nelle tecnologie quotidiane come motori a combustione e spray, e nei processi naturali come le gocce di pioggia e nella formazione delle nuvole. Gli esiti della collisione dipendono dalla velocità di impatto, grado di allineamento, proprietà intrinseche della tensione superficiale e una superficie a bassa bagnabilità. In un nuovo rapporto su Progressi scientifici , Olinka Ramírez-Soto e un team di scienziati nella ricerca sui polimeri, fluidodinamica, ingegneria chimica e dei materiali in Germania, I Paesi Bassi e gli Stati Uniti hanno studiato la dinamica di una goccia d'olio che colpisce una gocciolina sessile identica su una superficie superfifobica. Una superficie superanfifoba è analoga alla superidrofobicità (idrorepellenza), sebbene possa respingere sia liquidi polari che non polari. Utilizzando simulazioni numeriche, il team ha ricreato scenari di rimbalzo per quantificare i profili di velocità, trasferimento di energia e dissipazione viscosa nel setup sperimentale. Questo lavoro ha mostrato l'influenza della velocità d'impatto sulla dinamica di rimbalzo per le collisioni goccia a goccia d'olio su superfici superfifobiche.
Indagare sull'impatto del drop-on-drop
Quando una goccia di liquido colpisce una goccia sessile di un liquido identico, l'aspettativa intuitiva è che entrambe le gocce si uniscano o si combinino. Questo processo è comune con la pioggia e le gocce di un rubinetto che perde, ma a volte un sottile strato d'aria tra due gocce può invece consentire alle gocce d'acqua di rimbalzare perfettamente dalle superfici idrofile (amante dell'acqua). Nel 1800, lo scienziato e ingegnere Osborn Reynolds registrò e attribuì a questo fenomeno il movimento di scorrimento delle gocce d'acqua attraverso una piscina. Uno strato di vapore è similmente responsabile dell'effetto Leidenfrost, dove una goccia si libra sopra una superficie surriscaldata.
Nonostante la caratterizzazione sperimentale della dinamica di impatto, mancano metodi per modellare quantitativamente i campi di velocità e il trasferimento di energia. Gli studi sull'impatto della caduta su superfici superanfifobiche sono attualmente ostacolati da un numero limitato di tecniche per progettare superfici non bagnabili. È quindi importante capire quali scenari determinano l'impatto goccia su goccia dell'olio su una superficie superfifobica e come l'energia viene trasferita tra le gocce. In questo studio, Ramirez-Soto et al. studiato sperimentalmente e numericamente la dinamica di una goccia d'olio a bassa tensione superficiale che impatta su un liquido sessile di composizione simile appoggiato su una superficie superfifoba. Il team ha mostrato come la goccia d'olio impattante potrebbe sollevare la gocciolina a riposo dalla superficie senza fondersi.
Istantanee delle dinamiche di impatto. Notare che le etichette di caduta 1 e 2 sono per la caduta impattante e sessile, rispettivamente. Si osservano sei risultati (casi da I a VI) quando si varia il parametro di impatto e il numero di Weber (We). Le righe corrispondono a diversi parametri di impatto da I a IV. Le colonne mostrano le fasi caratteristiche del processo di collisione. UN, solo alla collisione; B, caduta sessile alla massima compressione; C, forma delle goccioline appena prima della separazione o della coalescenza; D, risultato finale dell'impatto. L'altezza del centro di massa dell'urto, sessile, o le gocce coalizzate è massima. Il volume di entrambe le gocce è di 3 μl. Caso I:We =1,30 e =0,01 i timestamp per ogni frame sono tA =0 ms, tB =8 ms, tC =20 ms, e tD =25 ms. Caso II:Noi =1,53, =0,08; tA =0 ms, tB =8 ms, tC =20 ms, e tD =24 ms. Caso III:Noi =1,44, =0,24; tA =0 ms, tB =8 ms, tC =20 ms, e tD =24 ms. Caso IV:We =1,48, =0,52; tA =0 ms, tB =5,5 ms, tC =7 ms, e tD =21 ms. Caso V:Noi =5,84, =0,08; tA =0 ms, tB =3,75 ms, tC =8,5 ms, e tD =25,5 ms. Caso VI:Noi =1.43, =0,03; tA =0 ms, tB =7,5 ms, tC =9 ms, e tD =17 ms. Credito fotografico:Olinka Ramírez-Soto, Istituto Max Planck per la ricerca sui polimeri. Credito:progressi scientifici, doi:10.1126/sciadv.aba4330 
Gli scienziati hanno condotto quattro esperimenti di rimbalzo senza coalescenza. Nel primo scenario, entrambe le gocce rimbalzano; in altri due scenari, la goccia impattante rimbalza mentre la goccia sessile rimane, e nello scenario finale la goccia sessile rimbalza mentre la goccia impattante rimane vincolata alla superficie. Durante gli esperimenti, Ramirez-Soto et al. posizionò delicatamente una goccia di olio sessile su una superficie superfifoba e la impattò con una seconda goccia identica. Hanno creato la superficie superfifobica utilizzando uno strato di 20 µm di fuliggine modellata per candele, che conteneva una rete porosa di nanosfere di carbonio. Per aumentare la stabilità della rete fragile, hanno depositato uno strato di silice sulle nanostrutture porose. Hanno abbassato l'energia superficiale della superficie a forma di fuliggine attraverso la fluorurazione per produrre una superficie superfifobica che respingeva l'acqua e la maggior parte degli oli. Gli scienziati hanno utilizzato l'esadecano come olio modello durante gli esperimenti a causa di una miriade di proprietà favorevoli tra cui il comportamento newtoniano e hanno registrato l'angolo di una goccia di esadecano utilizzando la microscopia confocale. Lo studio ha confrontato quantitativamente i dati sperimentali e numerici della dinamica di rimbalzo. Ramirez-Soto et al. calcolato e confermato il valore della forma della goccia utilizzando l'equazione di Young-Laplace.

Video sperimentale del Caso I per le gocce di esadecano:rimbalzo di una goccia d'urto. (numero Weber -
Risultati sperimentali e simulazioni numeriche.
Il team ha osservato sei risultati per le dinamiche di impatto. Durante l'impatto, entrambe le gocce si sono deformate e si sono allargate radialmente per mostrare la compressione assiale, mentre l'energia cinetica del sistema si è trasferita alle energie superficiali di entrambi. Quando le gocce cominciarono a ritirarsi, la goccia precedentemente sessile ha trasferito energia alla goccia d'urto sotto forma di energia cinetica. Dopo la collisione, la goccia impattante rimbalzò via, mentre la goccia sessile rimaneva sul substrato. Gli scienziati hanno mantenuto un numero Weber costante ( Noi ~ 1.5) per tutti e sei i casi osservati; dove il parametro tipicamente caratterizzava la qualità di atomizzazione di uno spray o la dimensione delle gocce risultanti delle emulsioni. Hanno quindi tracciato l'allineamento frontale (indicato con X) e aumentato il numero di Weber per la coalescenza delle gocce nella configurazione sperimentale. Hanno attribuito il risultato all'instabilità dello strato d'aria tra le gocce a causa del contatto diretto nelle condizioni sperimentali.
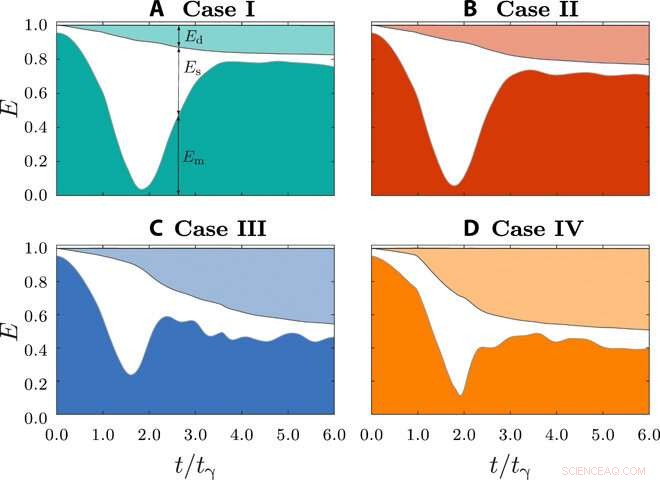
Bilancio energetico. La variazione temporale del trasferimento di energia chiarisce le diverse fasi del processo di impatto drop-on-drop a We ~1. Inizialmente, tutta l'energia viene immagazzinata come energia meccanica della goccia d'urto ed energia superficiale della goccia sessile. Quindi, l'energia meccanica del sistema diminuisce e viene trasferita nell'energia superficiale delle gocce. Questo trasferimento è seguito da una fase di recupero in cui l'energia superficiale viene trasferita nuovamente all'energia meccanica del sistema. Una parte dell'energia viene persa come dissipazione viscosa. Questa dissipazione viscosa considera l'energia combinata dissipata sia nelle gocce di liquido che nell'aria circostante. Questo calcolo include gli strati d'aria tra le gocce e tra le gocce e il substrato superfifobico. Durante l'impatto, le gocce (A) caso I:χ =0, (B) caso II:χ =0,08, (C) caso III:χ =0,25, e (D) caso IV:=0,625. Em è l'energia meccanica totale del sistema (Em =Ek + Ep), Es è l'energia superficiale delle due gocce, e Ed è la dissipazione viscosa nel sistema. Si noti che l'energia meccanica totale (Em) include l'energia del centro di massa delle gocce così come le energie di oscillazione e rotazione ottenute nel sistema di riferimento che sta traslando con il centro di massa delle singole gocce. Credito:progressi scientifici, doi:10.1126/sciadv.aba4330
Ramirez-Soto et al. ha quindi condotto simulazioni numeriche dirette (DNS) per illustrare l'effetto dei campi di velocità e trasferimento di energia tra le gocce e ha confrontato i risultati con i dati sperimentali. Il team ha utilizzato il metodo del volume geometrico del fluido (VOF) e ha preservato uno strato d'aria finito tra le gocce durante tutto il processo per imitare le condizioni sperimentali e ottenere goccioline non coalescenti mediante simulazioni. Il team ha eseguito le prime quattro simulazioni e quantificato i campi del vettore di velocità per ciascun caso; i risultati consentiranno di esplorare quantitativamente le dinamiche del processo di collisione drop-on-drop dell'olio.
Bilancio energetico
In tutti i casi, la goccia d'urto conteneva energia come energia meccanica (sotto forma di energia cinetica e potenziale) e come energia superficiale della goccia sessile. L'energia meccanica del sistema è quindi diminuita e trasferita nell'energia superficiale delle goccioline combinate. Al trasferimento è seguita una fase di recupero, in cui l'energia superficiale viene restituita all'energia meccanica del sistema, mentre una parte dell'energia dissipata sotto forma di dissipazione viscosa. Questo processo spiegava l'energia combinata dissipata nelle gocce di liquido e nell'aria circostante. I calcoli hanno anche tenuto conto dello strato d'aria tra il contatto goccia su goccia e tra il substrato goccia su superanfifobico. Le simulazioni numeriche hanno fornito una descrizione quantitativa delle dinamiche di impatto, where a strong agreement existed between the drop boundaries and experimental mechanical energies.

Experimental video of Case V (five) for hexadecane drops:coalescence of drops and lift-off of coalesced drop. Credito:progressi scientifici, doi:10.1126/sciadv.aba4330
In questo modo, Olinka Ramírez-Soto and colleagues combined systematic experiments and numerical simulations to predict and control the outcome of binary oil drop impacts on low-adhesion surfaces. The experimental and numeric one-on-one comparisons revealed the drop boundaries and center of mass mechanical energies, while illustrating the power of direct numerical simulations. The study highlighted how the alignment of droplet impact alone could be used to determine the recovered energy distribution between two drops after impact.
© 2020 Scienza X Rete