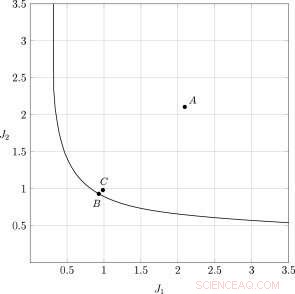
Un fronte ottimale di Pareto per il sistema a un grado di libertà. Credito:Università Lobachevsky
Oggigiorno le parole "incertezza" e "multicriterio" caratterizzano nel modo migliore la rilevanza e la complessità dei moderni problemi di gestione di una varietà di oggetti e processi dinamici.
Infatti, qualsiasi modello matematico che descriva processi controllati complessi include inevitabilmente imprecisioni nella descrizione dei disturbi esistenti e dei parametri dell'oggetto sotto controllo. Ignorare tale "incertezza" porta spesso a errori fatali nel funzionamento dei sistemi di gestione reali. D'altra parte, i diversi requisiti per il sistema di gestione sono generalmente contraddittori. Questo porta all'elaborazione di compiti multicriterio, che in caso di soluzione vincente consentono l'esclusione di soluzioni almeno note “inefficienti”.
È noto che le attività di gestione multicriterio sono molto difficili da eseguire. Queste difficoltà sono molte volte amplificate a causa dell'incertezza nell'impostazione dei disturbi attuali. Così, lo sviluppo della teoria e dei metodi per risolvere questi problemi sembra essere rilevante sia negli aspetti teorici che applicativi.
Secondo il professore dell'Istituto di tecnologie dell'informazione, Matematica e Meccanica Dr. Dmitry V. Balandin, l'oggetto dello studio è un sistema di equazioni differenziali ordinarie o alle derivate parziali. Si presume che un oggetto dinamico sia soggetto a influenze esterne, rispetto al quale si sa solo che appartiene a una data classe. Inoltre, anche le condizioni iniziali del sistema in esame sono assunte come incognite e appartenenti ad un dato insieme.
"Gli indicatori che caratterizzano i transitori per l'intera classe di influenze esterne e condizioni iniziali, chiamate deviazioni massime delle uscite del sistema, sono introdotte per il sistema in esame. In sostanza, questi indicatori determinano la risposta massima del sistema alla "peggiore" (più pericolosa) esposizione esterna e allo stato iniziale, " ha ricordato il prof. Balandin.
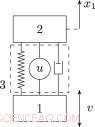
Schema di una protezione da urti e vibrazioni (sistema a un grado di libertà). Credito:Università Lobachevsky
Di conseguenza, vengono proposti nuovi metodi e algoritmi per la soluzione numerica di problemi di sintesi delle leggi di controllo ottimo di oggetti dinamici sotto forma dell'inverso con i criteri sotto forma di deviazioni massime degli output del sistema. Come applicazione, viene considerata una nuova classe di problemi di protezione ottimale dagli urti da vibrazioni di oggetti elastici, i cui criteri sono la massima deformazione dell'oggetto elastico di protezione e la massima deformazione del dispositivo antivibrante. I compiti consistono nel trovare feedback che caratterizzino l'assorbitore di vibrazioni e minimizzare i criteri sopra menzionati in Pareto. Per risolvere questa classe di problemi, l'approccio sopra menzionato viene applicato a problemi di controllo ottimo utilizzando la convoluzione di Hermeier e la tecnica delle disequazioni matriciali lineari.
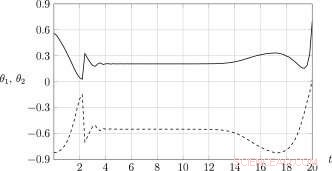
Storie temporali dei coefficienti ottimali di feedback di stato per il sistema a singolo grado di libertà. Credito:Università Lobachevsky
Viene considerato in dettaglio il compito a due criteri di protezione ottimale dalle vibrazioni di un grattacielo a più piani dagli impatti sismici e del vento. Si costruisce un insieme di Pareto, nonché un confronto del Pareto "ideale" dell'isolante ottimale, cioè il dispositivo di controllo, il cui feedback presuppone la presenza di informazioni attuali su tutte le variabili dello stato del sistema meccanico in esame, con gli isolanti ottimali di tipo attivo e passivo aventi una struttura più semplice del dispositivo di controllo.
L'applicazione dei metodi sviluppati di sintesi delle leggi del controllo multicriterio ottimale ai problemi di ottimizzazione dei sistemi di protezione dagli urti contro le vibrazioni è pionieristica e contribuisce a un progresso significativo nella teoria e nella pratica della protezione dagli urti contro le vibrazioni.