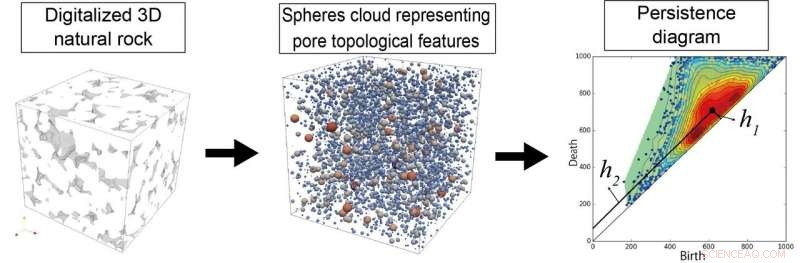
Figura:a sinistra:questa è una roccia naturale 3D digitalizzata, Centro:nuvola di sfere che rappresenta le caratteristiche topologiche dei pori, A destra:diagramma di persistenza. Credito:Istituto internazionale per la ricerca sull'energia a emissioni zero (I2CNER) / Istituto di matematica per l'industria (IMI), Università di Kyushu
Sulla base della teoria dell'omologia persistente, ricercatori dell'Università giapponese di Kyushu hanno presentato un nuovo parametro e un nuovo metodo per valutare l'eterogeneità della porosità
Fukuoka, Giappone:che ce ne rendiamo conto o no, la matematica permea le nostre vite in innumerevoli modi. Qualche volta, il ruolo della matematica è difficile da afferrare, ma altre volte è solido come una roccia.
Sebbene i grani minerali che formano una roccia siano importanti, sono i pori - gli spazi vuoti tra quei grani - che spesso trasportano risorse vitali come petrolio, gas, e acqua potabile. La geometria dei pori può influenzare fortemente lo stoccaggio, flusso, ed estrazione di tali risorse. Così, migliorare la comprensione della geometria dei pori è di grande interesse per molti ricercatori e professionisti del settore.
In una fusione di matematica e scienze della terra, i ricercatori dell'International Institute for Carbon-Neutral Energy Research (I2CNER) e dell'Institute of Mathematics for Industry (IMI) della Kyushu University hanno ora sviluppato un metodo innovativo per caratterizzare la geometria dei pori, basato su un concetto chiamato teoria dell'omologia persistente, come riportato in uno studio pubblicato su Ricerca sulle risorse idriche .
Un'importante differenza tra rocce naturali e mezzi artificiali è che le caratteristiche fisiche della roccia tendono ad essere relativamente eterogenee. Questo metodo all'avanguardia è particolarmente utile per caratterizzare tale eterogeneità nei pori.
Il primo autore dello studio, Fei Jiang, spiega, "Nel metodo proposto, la complessa geometria dei pori viene prima trasformata in dati di nuvole sferiche. Quindi, dalla nuvola di punti viene calcolato un diagramma di persistenza. Un nuovo parametro, l'indice di distanza H come metrica, è derivato dal diagramma di persistenza, e si propone di caratterizzare il grado di eterogeneità della roccia."
È stata confermata una forte relazione tra eterogeneità e indice di distanza H. Inoltre, viene proposta una nuova equazione empirica che utilizza questa metrica H per prevedere il modulo elastico effettivo delle rocce.
"Per testare il metodo appena proposto basato sulla geometria delle rocce reali, quattro tipi di roccia con differenti strutture dei pori, di cui due carbonati e due arenarie, sono stati indagati, " Il coautore Takeshi Tsuji spiega. "L'analisi del diagramma di persistenza era più efficace per stimare quantitativamente l'eterogeneità dell'arenaria relativamente omogenea rispetto al metodo convenzionale. Questo nuovo metodo era anche superiore in termini di distinzione dei diversi tipi di roccia".
Ulteriori vantaggi di questo metodo di analisi sono che il diagramma di persistenza è relativamente stabile con piccoli cambiamenti nello spazio dei pori, e l'indice di distanza H può essere calcolato in modo molto efficiente. Le informazioni estratte dall'analisi del diagramma di persistenza possono essere utilizzate per prevedere direttamente le proprietà fisiche (come permeabilità ed elasticità) in base alle microstrutture delle rocce. Così, l'analisi del diagramma di persistenza può rivelarsi un nuovo importante strumento per comprendere l'eterogeneità dei pori in diversi tipi di roccia.