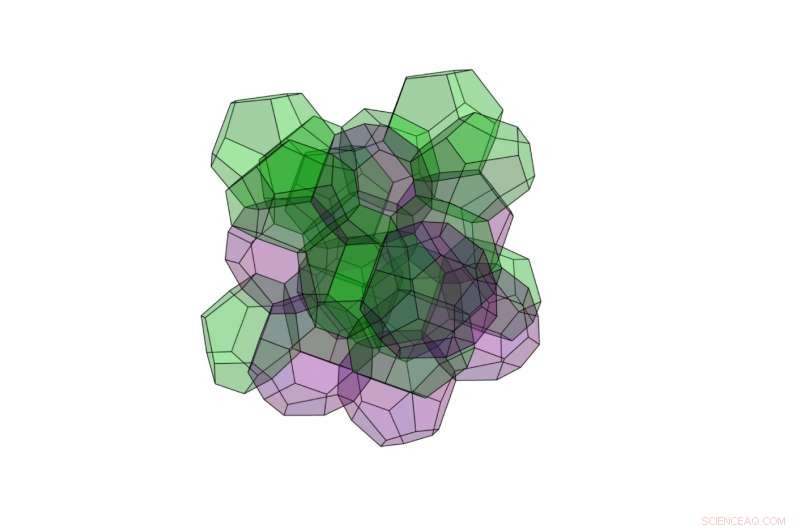
Una delle nuove strutture 3D ha la superficie più bassa di qualsiasi struttura di partizione spaziale conosciuta:è composta da 24 poliedri, alcuni dei quali hanno 12 facce e alcuni hanno 16 facce. Poiché i poliedri a 12 e 16 facce qui hanno volumi diversi, la nuova struttura non soddisfa il requisito originale di Kelvin per volumi uguali. Credito:Opsomer e Vandewalle. ©2016 IOP Publishing
(Phys.org)—I ricercatori hanno scoperto una nuova struttura 3D che divide lo spazio in 24 regioni, e hanno dimostrato che è la migliore soluzione finora per una versione modificata di un problema di partizionamento geometrico dello spazio che ha sfidato i ricercatori per più di un secolo.
Nel 1887, Lord Kelvin ha chiesto come è possibile suddividere lo spazio in strutture 3D di uguale volume in modo da ridurre al minimo la superficie totale di ciascuna struttura. Deve essere possibile unire insieme molte di queste strutture senza spazi tra loro, in altre parole, devono essere strutture "che riempiono lo spazio". Ogni struttura può assumere una varietà di forme 3D complesse, o "poliedri, " sia come singolo poliedro che come combinazione di più poliedri più piccoli di vario tipo. La sfida è capire quali particolari tipi di poliedri utilizzare per ridurre al minimo la superficie esterna dell'intera struttura.
La migliore soluzione di Kelvin a questo problema era un singolo poliedro chiamato "tetrakaidecahedron, " che ha 14 facce:sei quadrati e otto esagoni. Poiché questa è la forma ottenuta tagliando gli angoli di un diamante 3D, può anche essere pensato come un ottaedro troncato.
Sebbene la soluzione di Kelvin sia rimasta in piedi per più di un secolo, nel 1994 Denis Weaire e Robert Phelan del Trinity College di Dublino hanno utilizzato simulazioni numeriche per scoprire una partizione spaziale più ottimale. La soluzione di Weaire e Phelan è composta da otto poliedri di due tipi diversi, sebbene entrambi i tipi abbiano lo stesso volume:sei del tetrakaidecaedro di Kelvin e due dodecaedri (che ha 12 facce). Insieme, questi otto poliedri costituiscono una struttura 3D che ha un'area superficiale inferiore dello 0,3% rispetto al singolo tetracaidecaedro di Kelvin. La struttura Weaire-Phelan è rimasta la soluzione ottimale al problema di Kelvin negli ultimi 22 anni.
Ora nel nuovo studio, i fisici Eric Opsomer e Nicolas Vandewalle dell'Università di Liegi in Belgio hanno sviluppato un nuovo algoritmo per trovare strutture poliedriche composite che riempiono lo spazio con un'area superficiale minima.
Utilizzando il nuovo metodo, hanno scoperto che una nuova struttura 3D composta da 24 poliedri ha un'area superficiale ancora inferiore rispetto alla struttura Weaire-Phelan. I 24 poliedri sono di due tipi diversi:alcuni hanno 12 facce e alcuni hanno 16 facce. A differenza della struttura Weaire-Phelan, in cui i due diversi tipi di poliedri hanno volumi uguali, i poliedri a 12 e 16 facce qui hanno volumi significativamente differenti. Per questa ragione, la nuova struttura non soddisfa l'esigenza originaria di Kelvin di volumi uguali.
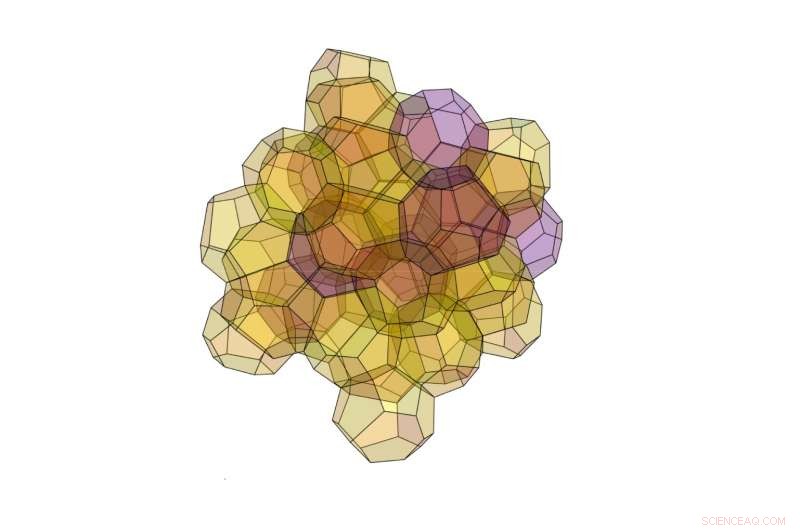
Il nuovo algoritmo ha scoperto questa struttura 3D composta da 40 poliedri di due diversi tipi. Credito:Opsomer e Vandewalle. ©2016 IOP Publishing
"Sfortunatamente, non è una 'vera soluzione, ' poiché le celle di volume uguale sono un requisito per il problema Kelvin originale, " ha detto Opsomer Phys.org . Ciò nonostante, la struttura è comunque interessante per altri motivi. "Questi risultati possono portare alla scoperta di strutture con potenziali implicazioni per la fisica dei materiali, ricerca medica, e altre aree, " ha detto Opsomer.
Come hanno spiegato i ricercatori, hanno intenzionalmente rimosso il vincolo dei volumi uguali quando hanno sviluppato il loro metodo di ricerca perché ha permesso loro di progettare l'algoritmo in un modo nuovo:invece di minimizzare direttamente la superficie di una struttura, hanno massimizzato gli isoperimetri medi dei poliedri (i perimetri condivisi da tutti i poliedri adiacenti). Sebbene questi due approcci siano diversi, sono in definitiva equivalenti.
I ricercatori hanno utilizzato il nuovo algoritmo per esplorare diverse strutture 3D composte da due a 64 poliedri. A partire da un numero specifico di punti disposti casualmente nello spazio 3D, l'algoritmo inizia a spostare i punti. Dopo ogni iterazione, l'algoritmo calcola il nuovo isoperimetro medio, e in base al risultato mantiene o rifiuta la nuova configurazione con una certa probabilità. Dopo milioni e talvolta miliardi di iterazioni, i punti alla fine formano i vertici di più poliedri che insieme formano una struttura 3D con superficie molto bassa.
Poiché attualmente non c'è modo di dimostrare quale sia la struttura di partizionamento spaziale più ottimale (con o senza celle di uguale volume), i ricercatori intendono continuare a cercare un'ampia varietà di strutture di tutti i tipi. La loro ipotesi migliore è che esistano strutture ancora più ottimali, e hanno intenzione di usare il loro algoritmo per continuare la loro esplorazione.
I ricercatori si aspettano anche che l'algoritmo possa generare altre strutture uniche. Una struttura particolarmente interessante che hanno scoperto qui è una struttura di 40 poliedri che è più ottimale della struttura di Kelvin ma non altrettanto buona della struttura Weaire-Phelan. Questa struttura altamente complessa è anche insolita in quanto non appartiene a una categoria di strutture chiamate strutture Frank-Kasper, su cui i ricercatori si sono tradizionalmente concentrati per una partizione ottimale dello spazio. La scoperta suggerisce che possono esistere anche altre strutture ottimali al di fuori di questa categoria.
Sebbene il problema di Kelvin non fosse stato originariamente proposto per soddisfare alcuna esigenza pratica, il partizionamento ottimale dello spazio ora ha una varietà di applicazioni. In campo medico, questi concetti sono stati usati per progettare forti, sostituzioni di tessuto osseo leggero. La suddivisione ottimale dello spazio ha ispirato anche l'architettura, con un esempio degno di nota è il luogo di nuoto costruito per le Olimpiadi di Pechino 2008. L'edificio, che si chiama Cubo d'Acqua, si basa sulla struttura Weaire-Phelan.
© 2016 Phys.org