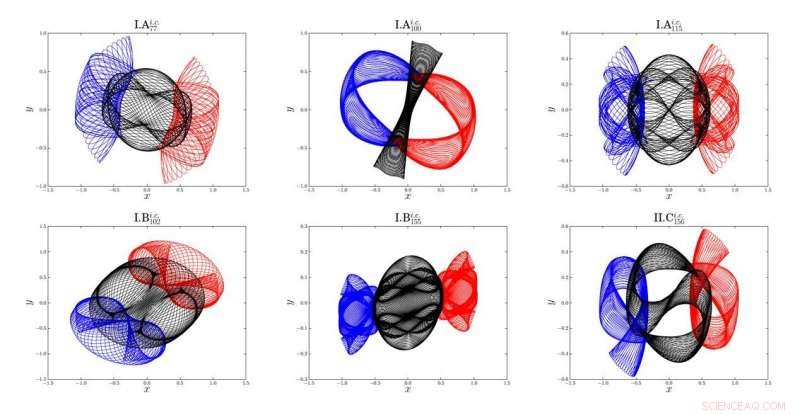
Breve panoramica delle sei famiglie ritrovate di orbite periodiche a tre corpi. Linea blu:orbita del Corpo-1; linea rossa:orbita del Corpo-2; linea nera:orbita di Body-3 Credito:©Science China Press
Il famoso problema dei tre corpi può essere fatto risalire a Isaac Newton nel 1680. Gli studi sul problema dei tre corpi hanno portato alla scoperta della cosiddetta dipendenza dalla sensibilità della condizione iniziale (SDIC) dei sistemi dinamici caotici. Oggi, le dinamiche caotiche sono ampiamente considerate come la terza grande rivoluzione scientifica in fisica nel XX secolo, paragonabile alla relatività e alla meccanica quantistica. Così, gli studi sul problema dei tre corpi hanno un significato scientifico molto importante.
Nel 1890, Poincaré determinò che le traiettorie dei sistemi a tre corpi sono comunemente non periodiche, cioè non ripetere. Questo può spiegare perché è così difficile ottenere le orbite periodiche dei sistemi a tre corpi. Nei 300 anni da quando il problema dei tre corpi è stato riconosciuto per la prima volta, erano state trovate solo tre famiglie di orbite periodiche. Nel 2013, Suvakov e Dmitrasinovic [ Fis. Rev. Lett. 110, 114301 (2013)] ha fatto un passo avanti, trovare 13 nuove orbite periodiche distinte appartenenti a 11 nuove famiglie del problema planare newtoniano a tre corpi con massa uguale e momento angolare nullo. Ora, due scienziati, XiaoMing Li e ShiJun Liao alla Shanghai Jiaotong University, Cina, hanno determinato con successo 695 famiglie di orbite periodiche dello stesso sistema planare newtoniano a tre corpi utilizzando il supercomputer TH-2 a Guangzhou, Cina. I loro risultati sono stati pubblicati in SCIENZA CINA-Fisica Meccanica e Astronomia . I video di queste orbite sono disponibili qui.
Queste 695 orbite periodiche includono la famosa famiglia di figure a otto trovata da Moore nel 1993, le 11 famiglie trovate da Suvakov e Dmitrasinovic nel 2013, e più di 600 nuove famiglie segnalate per la prima volta. I due scienziati hanno utilizzato la cosiddetta simulazione numerica pulita (CNS), una nuova strategia numerica per simulazioni affidabili di sistemi dinamici caotici proposta dal secondo autore nel 2009, che si basa su un ordine elevato di serie di Taylor e dati di precisione multipla, più un controllo di convergenza/affidabilità. Il SNC può ridurre gli errori di troncamento e gli errori di arrotondamento in modo così efficace che il rumore numerico è trascurabile in un intervallo di tempo sufficientemente lungo, così si possono ottenere orbite più periodiche del sistema dei tre corpi.
Come riportato da Montgomery nel 1998, ogni orbita periodica nello spazio reale del sistema dei tre corpi corrisponde ad una curva chiusa sulla cosiddetta "sfera di forma, " che si caratterizza per la sua topologia che utilizza il cosiddetto "elemento di gruppo libero". Il periodo medio di un'orbita è uguale al periodo dell'orbita diviso per la lunghezza del corrispondente elemento di gruppo libero. Queste 695 famiglie suggeriscono che il quadrato del periodo medio per il cubo dell'energia cinetica e potenziale totale è approssimativamente uguale a una costante La terza legge di Keplero generalizzata rivela che il sistema dei tre corpi ha qualcosa in comune che potrebbe approfondire la comprensione del sistema dei tre corpi.
Secondo gli scienziati, la scoperta delle oltre 600 nuove orbite periodiche è dovuta principalmente al progresso dell'informatica e all'uso della nuova strategia di simulazione numerica per sistemi dinamici caotici, vale a dire il SNC. Va sottolineato che altre 243 nuove orbite periodiche del sistema dei tre corpi si trovano tramite il SNC. In altre parole, se si utilizzassero algoritmi tradizionali a doppia precisione, circa il 40% delle nuove orbite periodiche andrebbe perso. Questo indica la novità e l'originalità del SNC, poiché ogni nuovo metodo deve offrire qualcosa di nuovo.