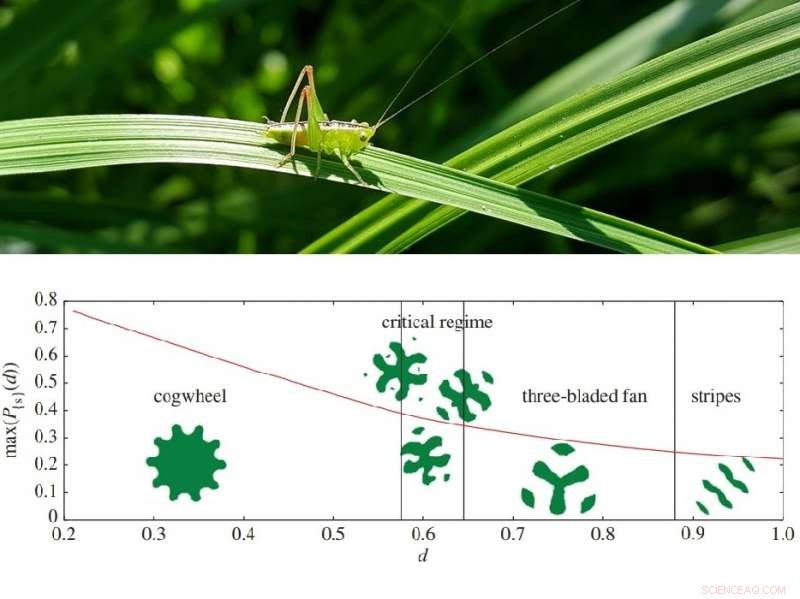
Alcune delle forme ottimali del prato, che dipendono dalla distanza per cui salta la cavalletta. Al di là del regime critico, le migliori configurazioni sono disconnesse. Credito diagramma:Goulko et al. La Società Reale. Credito:Pixabay.
(Phys.org)—Come molti enigmi matematici, il problema della cavalletta è semplice da enunciare ma difficile da risolvere:una cavalletta atterra in un punto casuale su un prato dell'area 1, poi salta una volta, una distanza fissa, in una direzione casuale. Che forma dovrebbe avere il prato per massimizzare la possibilità che la cavalletta rimanga sul prato dopo aver saltato?
Una prima impressione potrebbe essere che il prato debba avere la forma di un cerchio, almeno quando la distanza per cui salta la cavalletta è piccola. Però, Olga Goulko e Adrian Kent, i due fisici che hanno introdotto il problema delle cavallette in un nuovo articolo, hanno dimostrato matematicamente che un prato a forma di disco non è ottimale per nessuna distanza.
Anziché, hanno scoperto attraverso simulazioni numeriche che la forma ottimale del prato assume una varietà di forme complesse per diverse distanze di salto, come una forma di ruota dentata per distanze inferiori a 1/π 1/2 (il raggio di un cerchio di area 1, o circa 0,56), mentre per distanze maggiori, il prato ottimale è costituito da pezzi sconnessi. Spesso, ma non sempre, queste forme ottimali possiedono un qualche tipo di simmetria.
Motivato dalla fisica
Oltre ad essere un interessante problema di geometria, il problema della cavalletta è anche strettamente correlato alla ricerca in fisica quantistica e può avere una varietà di applicazioni tecnologiche. In particolare, il problema della cavalletta è connesso alle disuguaglianze di Bell, che notoriamente mostrano che, a differenza dei modelli fisici classici, la teoria quantistica non obbedisce al realismo locale. Un primo esempio della violazione del realismo locale è visto nell'entanglement quantistico, in cui due sistemi entangled distanti mostrano correlazioni che non possono essere spiegate da alcun modello che obbedisce al realismo locale.
Questa connessione alle disuguaglianze di Bell è, infatti, ciò che originariamente motivava Goulko e Kent a proporre il problema delle cavallette. Un problema aperto in fisica riguardo alle disuguaglianze di Bell è determinare i limiti ottimali che vengono violati dalla teoria quantistica quando le correlazioni quantistiche vengono misurate su una sfera ad angoli tra 0 e 90 gradi. Si scopre che questo problema di determinare i limiti ottimali è equivalente al problema di determinare la forma del prato del problema della cavalletta quando il prato è sferico anziché piatto. Nella versione sferica del problema della cavalletta, la distanza per cui la cavalletta salta su un terreno pianeggiante è sostituita dall'angolo con cui salta attraverso la sfera.
Nella loro carta, che è pubblicato in un recente numero del Atti della Royal Society A , Goulko e Kent hanno analizzato solo la versione planare del problema della cavalletta, sebbene si aspettino che non dovrebbe essere troppo difficile applicare le stesse tecniche numeriche al caso sferico. Quindi, quando si tiene conto di alcuni vincoli aggiuntivi, si potrebbe finalmente risolvere il problema dei limiti ottimi delle disuguaglianze di Bell.
"Abbiamo in programma di lavorare sulle versioni sferiche del problema della cavalletta relative alle disuguaglianze di Bell, e ci aspettiamo che i nostri metodi funzionino lì, "Kent ha detto Phys.org .
Nuova frontiera
Come spiegano i fisici, una delle cose sorprendenti del problema delle cavallette è che nulla di simile è mai stato proposto prima. Sebbene l'idea di base sia abbastanza semplice che il problema potrebbe essere stato posto dall'antico matematico greco Euclide, che ha posto le basi della moderna geometria, i ricercatori non sono a conoscenza di alcuna versione precedente del problema, sia in epoca antica che moderna.
"È bello ricordare che, anche in un campo antico come la geometria, si possono ancora trovare semplici domande nuove che hanno risposte sorprendenti e aprono nuove linee di ricerca, " ha detto Kent.
Come un problema nuovo di zecca, ci sono un numero infinito di direzioni di ricerca future da prendere. Ad esempio, i fisici suggeriscono di permettere alla cavalletta di fare più salti, o richiedere che la cavalletta cammini e rimanga sul prato in tutti i punti del suo percorso (una variante che chiamano il "problema delle formiche"). Altre possibili variazioni includono la generalizzazione a dimensioni superiori, analizzare le superfici del prato diverse da sfere e piani, considerando una variazione del problema con due diverse specie di semi di prato che possono sovrapporsi nella stessa regione (cosa particolarmente rilevante per le disuguaglianze di Bell), e ponendo ulteriori restrizioni alle possibili soluzioni.
Certo, tali domande non riguardano realmente cavallette e prati, poiché la struttura sottostante offre un modo per modellare varie situazioni del mondo reale. Un esempio che i ricercatori sottolineano sono le reazioni a catena nucleari. In una reazione a catena, una particella ad alta energia colpisce un nucleo atomico casuale, provocandone la fissione, che produce un'altra particella ad alta energia che percorre una certa distanza per colpire un altro nucleo casuale, e il processo si ripete. Modellando questa situazione con il problema della cavalletta, la superficie ottimale del prato corrisponde alla massima velocità di reazione iniziale, che massimizza il numero di nuclei che partecipano alla reazione a catena.
Un'altra potenziale applicazione del problema della cavalletta risiede nella modellazione dei protocolli di comunicazione quantistica, che i ricercatori spiegano può essere pensato come un modello di cavalletta in cui una parte deve scegliere quale algoritmo (forma di prato) utilizzare per comunicare con una seconda parte.
E infine, i ricercatori suggeriscono che potrebbe essere interessante esaminare le origini delle forme stesse del prato, poiché alcuni dei motivi del prato assomigliano a modelli che emergono ripetutamente in natura, come nei fiori, conchiglie, e strisce di animali. In accordo con la teoria della morfogenesi proposta da Alan Turing, questi modelli possono presentarsi come soluzioni ottimali per ragioni chimiche, che può aiutare a spiegare le diverse e complesse forme dei prati che compaiono nel problema della cavalletta.
© 2017 Phys.org