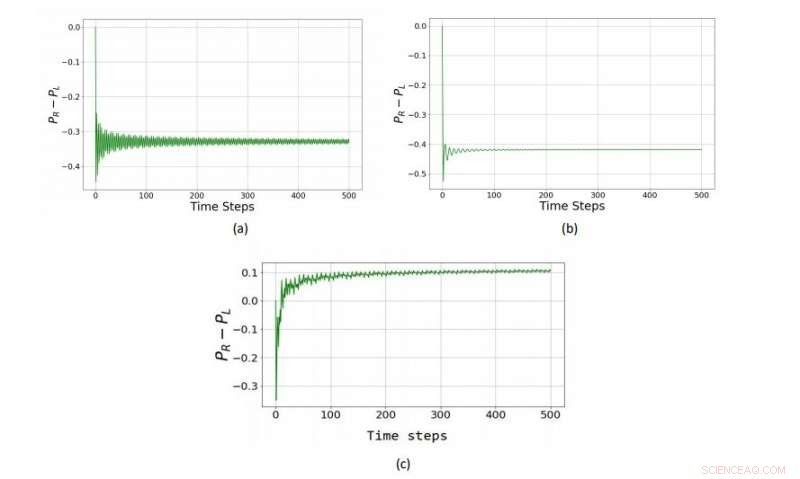
In una versione quantistica del gioco di Parrondo giocato con una moneta a tre stati (un qutrit), le due strategie perdenti (a) e (b) sono combinate in una strategia vincente (c). Credito:Rajendran et al. ©2018 EPL
I fisici hanno dimostrato che il paradosso di Parrondo - un apparente paradosso in cui due strategie perdenti si combinano per creare una strategia vincente - può emergere come un gioco di monete con una singola moneta nel regno quantistico, ma solo quando la moneta ha tre stati (teste, code, e un lato) piuttosto che i due convenzionali.
Generalmente, Il paradosso di Parrondo, chiamato anche gioco di Parrondo, funziona solo quando le due strategie perdenti sono in qualche modo dipendenti l'una dall'altra e sono combinate in modo tale da modificare le condizioni che le portano a perdere. Da quando è stato scoperto dal fisico Juan Parrondo nel 1996, Il paradosso di Parrondo ha trovato applicazioni in ingegneria, finanza, e biologia evolutiva, tra le altre aree.
Uno dei modi più semplici per implementare un gioco di Parrondo è descritto in questa voce di Wikipedia. Supponi di avere $ 100, e puoi scegliere di giocare a qualsiasi combinazione di due giochi. Nella prima partita, perdi $ 1 ogni volta che giochi. Nella seconda partita, vinci $ 3 se hai un numero pari di dollari rimasti, e perdi $ 5 se hai un numero dispari di dollari rimasti. Se giochi solo al primo gioco o giochi solo al secondo gioco, alla fine perderai tutti i tuoi soldi, quindi giocare ogni gioco da solo è una strategia perdente. Però, se si alternano i due giochi, a partire dalla seconda partita, allora vincerai $ 2 per ogni due giochi che giochi, quindi le due strategie perdenti possono combinarsi in una strategia vincente.
Nel nuovo studio, i fisici Jishnu Rajendran e Colin Benjamin presso l'Istituto Nazionale di Educazione e Ricerca Scientifica, HBNI, in India, hanno dimostrato un gioco di Parrondo usando una moneta a tre stati, che rappresentano con un qutrit, un sistema quantistico con tre stati.
"Le partite di Parrondo sono state viste in un contesto classico, "Benjamin ha detto Phys.org . "Il nostro obiettivo in questo lavoro era mostrare come implementarlo in un contesto quantistico, in particolare in una passeggiata quantistica. Sfortunatamente, la versione quantistica di questo gioco quando implementata con una singola moneta (qubit) in una passeggiata quantistica ha fallito nei limiti asintotici. Quello che mostriamo in questo lavoro è che un qutrit può implementare questo gioco di Parrondo in una passeggiata quantistica".
Nella passeggiata quantistica, un giocatore parte dall'origine e si sposta a destra (direzione positiva) oa sinistra (direzione negativa) a seconda del risultato del lancio della moneta. Se teste, il giocatore si muove a destra; se croce, sinistra; e se il risultato è "side, " quindi il giocatore lo interpreta come uno "stato di attesa" e rimane nello stesso posto. Poiché il qutrit è un sistema quantistico, può anche essere in una sovrapposizione di questi stati, nel qual caso il giocatore si sposta nella posizione corrispondente, da qualche parte tra un passo completo a sinistra oa destra. Alla fine del gioco, se la probabilità che il giocatore si trovi a destra dell'origine è maggiore della probabilità di trovarsi a sinistra dell'origine, il giocatore vince. Altrimenti, loro hanno perso.
Utilizzando alcuni dei metodi standard della fisica delle particelle per definire i concetti di lancio della moneta e regole del gioco con una sovrapposizione di stati, i fisici hanno dimostrato diversi esempi di giochi che risultano perdenti se giocati individualmente, ma quando combinati in una sequenza alternata danno un risultato vincente. Hanno anche dimostrato esempi del contrario. Per esempio, due partite che si traducono in una vittoria e in un pareggio se giocate individualmente possono portare a un risultato perdente se combinate.
I fisici hanno anche dimostrato che, sebbene non sia possibile implementare un gioco di Parrondo utilizzando una singola moneta a due facce (qubit), è possibile realizzare un gioco di Parrondo utilizzando due monete a due facce (due qubit). Gli stati aggiuntivi forniscono essenzialmente una flessibilità aggiuntiva con cui combinare strategie in grado di superare le condizioni di perdita.
Date le ampie applicazioni dei giochi classici di Parrondo, i fisici si aspettano che la versione quantistica possa portare a nuove informazioni sulla progettazione di algoritmi quantistici.
"Il gioco di Parrondo è una ricetta per dimostrare che non è necessario cercare sempre una strategia (o un algoritmo) vincente in un gioco, " Benjamin ha detto. "Classicamente, ci sono molte applicazioni dei giochi di Parrondo, che vanno dalla spiegazione dei processi fisiologici nella cellula all'aumento della nostra comprensione dei motori Browniani e persino all'investimento di portafogli diversificati. Classicamente, È stato dimostrato che il paradosso di Parrondo funziona utilizzando le classiche passeggiate casuali.
"Implementare un gioco di Parrondo in una passeggiata quantistica avrebbe implicazioni per l'elaborazione di algoritmi quantistici migliori o più veloci. Un algoritmo che utilizza principi quantistici come la sovrapposizione e/o l'entanglement è un algoritmo quantistico. Un algoritmo, se può essere implementato su una passeggiata quantistica, sarebbe più redditizio di uno che può essere implementato solo su una classica passeggiata casuale. Poiché le passeggiate quantistiche si diffondono quadraticamente più velocemente delle classiche passeggiate casuali, un algoritmo implementato su una passeggiata quantistica impiegherà un tempo molto più breve per essere completato rispetto a uno su una classica passeggiata casuale. Ulteriore, la riuscita implementazione del gioco di Parrondo su una passeggiata quantistica fornisce una spiegazione algoritmica per i cricchetti quantistici [sistemi che hanno movimento in una sola direzione]."
© 2018 Phys.org