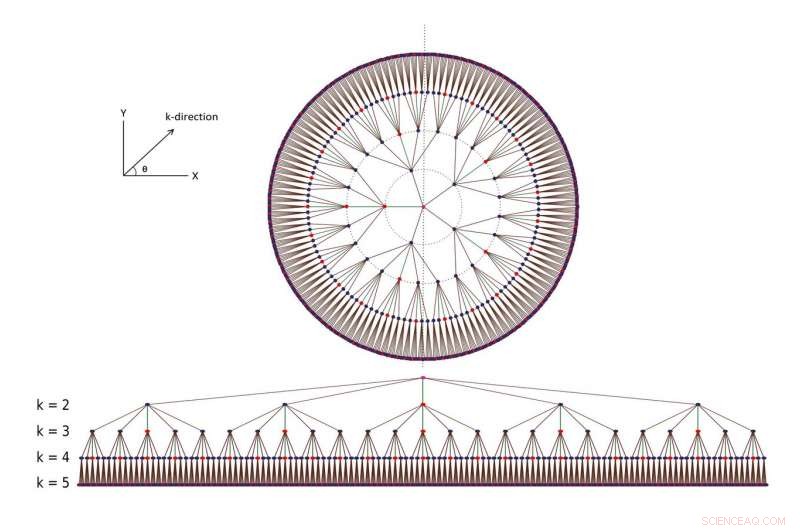
Il circuito quantistico. Strati diversi corrispondono a tolleranze di errore diverse, con lo strato inferiore che ha la tolleranza di errore più piccola. Credito:Autori/Lettere di revisione fisica
circuiti quantistici, gli elementi costitutivi dei computer quantistici, utilizzare gli effetti della meccanica quantistica per eseguire le attività. Sono molto più veloci e precisi dei circuiti classici che si trovano oggi nei dispositivi elettronici. In realtà, però, nessun circuito quantistico è completamente privo di errori. Massimizzare l'efficienza di un circuito quantistico è di grande interesse per gli scienziati di tutto il mondo.
I ricercatori dell'Indian Institute of Science (IISc) hanno ora affrontato questo problema utilizzando un analogo matematico. Hanno ideato un algoritmo per contare esplicitamente il numero di risorse di calcolo necessarie, e ottimizzato per ottenere la massima efficienza.
"Siamo stati in grado di [teoricamente] costruire il circuito più efficiente e ridurre la quantità di risorse necessarie per un fattore enorme, "dice Aninda Sinha, Professore Associato presso il Centro di Fisica delle Alte Energie, IISc, e corrispondente autore dell'articolo pubblicato in Lettere di revisione fisica . I ricercatori suggeriscono anche che questa sia la massima efficienza possibile ottenibile per un circuito quantistico.
L'ottimizzazione dell'efficienza del circuito quantistico è utile in vari campi, soprattutto informatica quantistica. Non solo i computer quantistici forniranno risultati più rapidi e accurati rispetto ai computer classici, saranno anche più sicuri:non possono essere hackerati, che li rende utili per la protezione contro le frodi bancarie digitali, violazioni della sicurezza e furto di dati. Possono anche essere utilizzati per affrontare compiti complicati come l'ottimizzazione dei problemi di trasporto e la simulazione del mercato finanziario.
I circuiti classici sono costituiti da porte logiche universali (come le porte NAND e NOR), ognuno dei quali esegue operazioni predefinite sull'input per produrre un output.
"Analogamente, ci sono porte quantistiche universali per realizzare circuiti quantistici. In realtà, i cancelli non sono efficienti al 100%; c'è sempre un errore associato all'uscita di ogni porta. E quell'errore non può essere rimosso; continua semplicemente ad aggiungere per ogni porta utilizzata nel circuito, "dice Pratik Nandy, Il dottorato di Sinha studente e co-autore dell'articolo.
Il circuito più efficiente non minimizza l'errore in uscita; piuttosto riduce al minimo le risorse necessarie per ottenere lo stesso output. "Quindi la domanda si riduce a:data una tolleranza di errore netta, qual è il numero minimo di porte necessarie per costruire un circuito quantistico?" dice Nandy.
Nel 2006, uno studio condotto da Michael Nielsen, un ex membro di facoltà presso l'Università del Queensland, ha mostrato che contare il numero di porte per ottenere la massima efficienza equivale a trovare il percorso con la distanza più breve tra due punti in uno spazio matematico con volume V. Uno studio separato del 2016 ha sostenuto che questo numero dovrebbe variare direttamente con V.
"Siamo tornati al lavoro originale di Nielsen e si scopre che il suo conteggio delle porte non ti dà una variazione con V, piuttosto varia con V 2 , " dice Sinha. Lui e il suo team hanno generalizzato le ipotesi di quello studio e introdotto alcune modifiche per risolvere il problema di ottimizzazione. "I nostri calcoli hanno rivelato che il numero minimo di porte in effetti varia direttamente con il volume, " lui dice.
Sorprendentemente, i loro risultati sembrano anche collegare il problema di ottimizzazione dell'efficienza con la teoria delle stringhe, una famosa idea che cerca di combinare la gravità e la fisica quantistica per spiegare come funziona l'universo. Sinha e il suo team ritengono che questo collegamento possa rivelarsi determinante nell'aiutare gli scienziati a interpretare le teorie che coinvolgono la gravità. Mirano inoltre a sviluppare metodi che descrivono una raccolta di circuiti quantistici per calcolare determinate quantità sperimentali che non possono essere simulate teoricamente utilizzando i metodi esistenti.