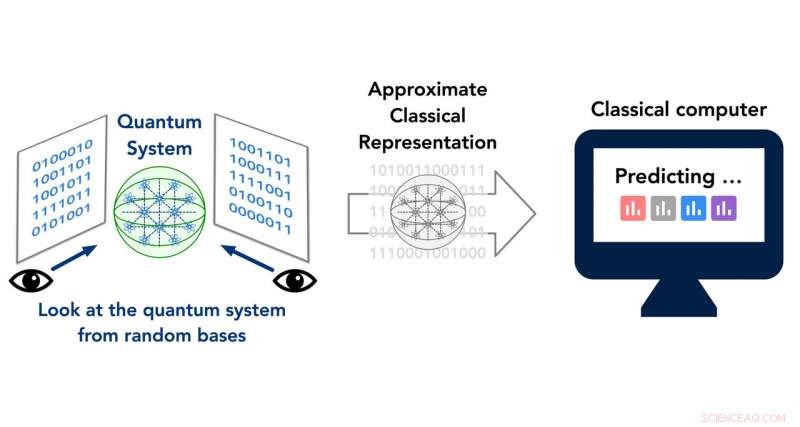
Credito:Huang, Kueng e Preskill.
La previsione delle proprietà di sistemi quantistici complessi è un passaggio cruciale nello sviluppo di tecnologie quantistiche avanzate. Mentre i gruppi di ricerca di tutto il mondo hanno già ideato una serie di tecniche per studiare le caratteristiche dei sistemi quantistici, la maggior parte di questi si è dimostrata efficace solo in alcuni casi.
Tre ricercatori del California Institute of Technology hanno recentemente introdotto un nuovo metodo che può essere utilizzato per prevedere proprietà multiple di sistemi quantistici complessi da un numero limitato di misurazioni. Il loro metodo, delineato in un articolo pubblicato su Fisica della natura , si è rivelato altamente efficiente e potrebbe aprire nuove possibilità per studiare i modi in cui le macchine elaborano le informazioni quantistiche.
"Durante il mio corso di laurea, la mia ricerca si è incentrata sul machine learning statistico e sul deep learning, "Hsin Yuan Huang, uno dei ricercatori che ha condotto lo studio, ha detto a Phys.org. "Una base centrale per l'attuale era del machine learning è la capacità di utilizzare hardware altamente parallelizzato, come unità di elaborazione grafica (GPU) o unità di elaborazione del tensore (TPU). È naturale chiedersi come potrebbe emergere in un lontano futuro una macchina per l'apprendimento ancora più potente in grado di sfruttare i processi quantomeccanici. Questa era la mia aspirazione quando ho iniziato il mio dottorato di ricerca. al Caltech."
Il primo passo verso lo sviluppo di macchine più avanzate basate su processi quantomeccanici è acquisire una migliore comprensione di come le attuali tecnologie elaborano e manipolano i sistemi quantistici e le informazioni quantistiche. Il metodo standard per farlo, nota come tomografia a stato quantistico, funziona imparando l'intera descrizione di un sistema quantistico. Però, ciò richiede un numero esponenziale di misurazioni, così come una notevole memoria e tempo computazionale.
Di conseguenza, quando si utilizza la tomografia a stato quantistico, le macchine attualmente non sono in grado di supportare sistemi quantistici con più di decine di qubit. Negli ultimi anni, i ricercatori hanno proposto una serie di tecniche basate su reti neurali artificiali che potrebbero migliorare significativamente l'elaborazione delle informazioni quantistiche delle macchine. Sfortunatamente, però, queste tecniche non si generalizzano bene in tutti i casi, e non sono ancora chiari i requisiti specifici che consentono loro di lavorare.
"Per costruire una base rigorosa su come le macchine possono percepire i sistemi quantistici, abbiamo combinato le mie precedenti conoscenze sulla teoria dell'apprendimento statistico con l'esperienza di Richard Kueng e John Preskill su una bellissima teoria matematica nota come t-design unitario, " Huang ha detto. "La teoria dell'apprendimento statistico è la teoria che sta alla base di come la macchina potrebbe apprendere un modello approssimativo su come si comporta il mondo, mentre il t-design unitario è una teoria matematica che sta alla base del modo in cui le informazioni quantistiche si mescolano, che è fondamentale per comprendere il caos quantistico a molti corpi, in particolare, buchi neri quantistici".
Combinando l'apprendimento statistico e la teoria unitaria del t-design, i ricercatori sono stati in grado di ideare una procedura rigorosa ed efficiente che consente alle macchine classiche di produrre descrizioni classiche approssimative dei sistemi quantistici a molti corpi. Queste descrizioni possono essere utilizzate per prevedere diverse proprietà dei sistemi quantistici che vengono studiati eseguendo un numero minimo di misurazioni quantistiche.
"Per costruire una descrizione classica approssimata dello stato quantistico, eseguiamo una procedura di misurazione randomizzata data come segue, "Ha detto Huang. "Campioniamo alcune evoluzioni quantistiche casuali che verrebbero applicate al sistema quantistico sconosciuto a molti corpi. Queste evoluzioni quantistiche casuali sono tipicamente caotiche e confonderebbero le informazioni quantistiche memorizzate nel sistema quantistico".
Le evoluzioni quantistiche casuali campionate dai ricercatori alla fine consentono l'uso della teoria matematica del t-design unitario per studiare sistemi quantistici caotici come i buchi neri quantistici. Inoltre, Huang e i suoi colleghi hanno esaminato una serie di sistemi quantistici rimescolati casualmente utilizzando uno strumento di misurazione che provoca il collasso della funzione d'onda, un processo che trasforma un sistema quantistico in un sistema classico. Finalmente, hanno combinato le evoluzioni quantistiche casuali con le rappresentazioni del sistema classico derivate dalle loro misurazioni, producendo una descrizione classica approssimata del sistema quantistico di interesse.
"Intuitivamente, si potrebbe pensare a questa procedura come segue, " ha spiegato Huang. "Abbiamo un oggetto esponenzialmente ad alta dimensione, il sistema quantistico a molti corpi, che è molto difficile da afferrare da una macchina classica. Eseguiamo diverse proiezioni casuali di questo oggetto di dimensioni estremamente elevate in uno spazio dimensionale molto più basso attraverso l'uso dell'evoluzione quantistica casuale/caotica. L'insieme di proiezioni casuali fornisce un'immagine approssimativa di come appare questo oggetto dimensionale esponenzialmente alto, e la rappresentazione classica ci consente di prevedere varie proprietà del sistema quantistico a molti corpi".
Huang e i suoi colleghi hanno dimostrato che, combinando i costrutti di apprendimento statistico e la teoria del rimescolamento delle informazioni quantistiche, potrebbero prevedere con precisione le proprietà M di un sistema quantistico basato esclusivamente su misurazioni log(M). In altre parole, il loro metodo può prevedere un numero esponenziale di proprietà semplicemente misurando ripetutamente aspetti specifici di un sistema quantistico per un numero specifico di volte.
"La comprensione tradizionale è che quando vogliamo misurare M proprietà, dobbiamo misurare il sistema quantistico M volte, " disse Huang. "Questo perché dopo aver misurato una proprietà del sistema quantistico, il sistema quantistico collasserebbe e diventerebbe classico. Dopo che il sistema quantistico è diventato classico, non possiamo misurare altre proprietà con il sistema classico risultante. Il nostro approccio evita ciò eseguendo misurazioni generate casualmente e deducendo la proprietà desiderata combinando questi dati di misurazione".
Lo studio spiega in parte le eccellenti prestazioni ottenute dalle tecniche di machine learning (ML) recentemente sviluppate nella previsione delle proprietà dei sistemi quantistici. Inoltre, il suo design unico rende il metodo che hanno sviluppato significativamente più veloce rispetto alle tecniche ML esistenti, consentendo allo stesso tempo di prevedere le proprietà dei sistemi quantistici a molti corpi con una maggiore precisione.
"Il nostro studio mostra rigorosamente che ci sono molte più informazioni nascoste nei dati ottenuti dalle misurazioni quantistiche di quanto ci aspettassimo inizialmente, " Huang ha detto. "Combinando opportunamente questi dati, possiamo dedurre queste informazioni nascoste e acquisire una conoscenza significativamente maggiore sul sistema quantistico. Ciò implica l'importanza delle tecniche di data science per lo sviluppo della tecnologia quantistica".
I risultati dei test condotti dal team suggeriscono che per sfruttare la potenza dell'apprendimento automatico, è prima necessario acquisire una buona comprensione dei meccanismi intrinseci della fisica quantistica. Huang e i suoi colleghi hanno dimostrato che, sebbene l'applicazione diretta di tecniche standard di apprendimento automatico possa portare a risultati soddisfacenti, la combinazione organica della matematica alla base dell'apprendimento automatico e della fisica quantistica si traduce in prestazioni di elaborazione delle informazioni quantistiche di gran lunga migliori.
"Dato un terreno rigoroso per percepire i sistemi quantistici con le macchine classiche, il mio piano personale è ora di fare il prossimo passo verso la creazione di una macchina per l'apprendimento in grado di manipolare e sfruttare i processi quantomeccanici, " Huang ha detto. "In particolare, vogliamo fornire una solida comprensione di come le macchine potrebbero imparare a risolvere problemi quantistici a molti corpi, come classificare le fasi quantistiche della materia o trovare stati fondamentali quantistici a molti corpi".
Questo nuovo metodo per costruire rappresentazioni classiche di sistemi quantistici potrebbe aprire nuove possibilità per l'uso dell'apprendimento automatico per risolvere problemi impegnativi che coinvolgono sistemi quantistici a molti corpi. Per affrontare questi problemi in modo più efficiente, però, le macchine dovrebbero anche essere in grado di simulare una serie di calcoli complessi, che richiederebbe un'ulteriore sintesi tra la matematica alla base dell'apprendimento automatico e la fisica quantistica. Nei loro studi successivi, Huang ei suoi colleghi hanno in programma di esplorare nuove tecniche che potrebbero consentire questa sintesi.
"Allo stesso tempo, stiamo anche lavorando per perfezionare e sviluppare nuovi strumenti per dedurre informazioni nascoste dai dati raccolti dagli sperimentalisti quantistici, " Huang ha detto. "La limitazione fisica nei sistemi attuali offre sfide interessanti per lo sviluppo di tecniche più avanzate. Ciò consentirebbe inoltre agli sperimentali di vedere ciò che originariamente non potevano e contribuire a far progredire lo stato attuale della tecnologia quantistica".
© 2020 Scienza X Rete