Diversi esperimenti recenti identificano modelli insoliti nella diffusione delle particelle, suggerendo una certa complessità di fondo nel processo che i fisici devono ancora scoprire. Attraverso una nuova analisi pubblicata su The European Physical Journal B , Adrian Pacheco-Pozo e Igor Sokolov dell'Università Humboldt di Berlino mostrano come questo comportamento emerga attraverso forti correlazioni tra le posizioni delle particelle diffondenti che viaggiano lungo traiettorie simili.

I loro risultati potrebbero aiutare i ricercatori a creare modelli migliori del processo di diffusione, ottenendo in definitiva informazioni più approfondite sul comportamento dei fluidi.

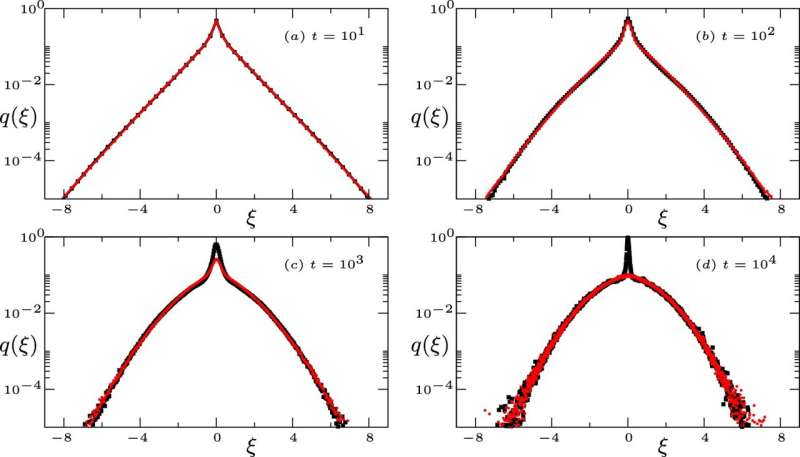
In molti casi, la diffusione avviene attraverso fluttuazioni casuali nella posizione delle particelle mentre vengono spinte dalle particelle vicine. Conosciuto come moto browniano, questo effetto può essere visualizzato matematicamente utilizzando la distribuzione normale:una curva a campana che illustra la probabilità di trovare una particella a qualsiasi spostamento dalla sua posizione iniziale. Tuttavia, in alcune situazioni, questa distribuzione può presentare un picco netto al centro, ovvero il vertice della curva a campana, dove la probabilità di trovare particelle è particolarmente alta.

Questo comportamento ha molto in comune con i modelli teorici caratterizzati da tassi di diffusione che variano tra regioni localizzate, dove, contrariamente all'aspettativa che il picco centrale si attenuerà nel tempo, in realtà si restringe e rimane acuto.

Nel loro studio, Pacheco-Pozo e Sokolov hanno studiato la natura di questo picco persistente considerando la matematica dei modelli di "camminata casuale in tempo continuo". In questo caso, una particella che si diffonde attende per un periodo di tempo casuale prima di saltare in una nuova posizione e più a lungo aspetta, più salta.

In questo caso, i due hanno dimostrato che un netto picco centrale emerge attraverso forti correlazioni tra gli spostamenti delle particelle che saltano seguendo traiettorie simili, sia nel tempo che nello spazio. Tuttavia, il modello di camminata casuale in tempo continuo non è riuscito a riprodurre pienamente la forma del picco acuto. Ciò suggerisce l'importanza di connessioni più complesse e variabili nel tempo tra le particelle, che i ricercatori sperano ora di indagare nei loro studi futuri.

Ulteriori informazioni: Adrian Pacheco-Pozo et al, Passeggiate casuali in paesaggi di diffusività correlati, The European Physical Journal B (2023). DOI:10.1140/epjb/s10051-023-00621-z

Informazioni sul giornale: Giornale fisico europeo B

Fornito da SciencePOD