Negli ultimi anni, i fisici hanno cercato di comprendere meglio il modo in cui le informazioni quantistiche si diffondono nei sistemi di particelle interagenti, un fenomeno spesso definito “scrambling”. La codifica in sistemi chiusi, sistemi fisici che possono scambiare energia solo con gradi di libertà all'interno del sistema, è una caratteristica della dinamica quantistica caotica a molti corpi.

Nei sistemi aperti, che possono scambiare sia energia che materia con l'ambiente circostante, lo scrambling è influenzato da vari fattori aggiuntivi, tra cui rumore ed errori. Sebbene gli effetti di queste influenze aggiuntive siano ben documentati, portando ad esempio alla decoerenza, il modo in cui influenzano lo scrambling rimane poco compreso.

Due ricercatori dell'Università della California Berkeley (UC Berkeley) e dell'Università di Harvard hanno recentemente introdotto un nuovo framework, pubblicato su Physical Review Letters , che fornisce un quadro universale di come avviene la codifica delle informazioni nei sistemi quantistici aperti. Il loro quadro offre un punto di vista particolarmente semplice su come comprendere e modellare la propagazione degli errori in un sistema quantistico aperto e potrebbe già aiutare a spiegare alcune osservazioni precedentemente sconcertanti raccolte negli esperimenti di risonanza magnetica.

"Norm e io abbiamo già lavorato insieme su diversi progetti concentrandoci sulla codificazione delle informazioni quantistiche", ha detto a Phys.org Thomas Schuster, uno dei ricercatori che hanno condotto lo studio.

"Alcuni dei nostri lavori si concentravano su come misurare lo scrambling, altri su a cosa potrebbe essere utile. In tutti questi progetti, continuava a sorgere una domanda naturale:come viene modificato lo scrambling dagli errori (ovvero, il sistema 'a sistema aperto') dinamiche) che inevitabilmente si verificano negli esperimenti nella vita reale? Sebbene questa domanda fosse chiaramente importante, non disponevamo di un quadro soddisfacente per rispondere."

Esplorando questa domanda, Schuster e Yao si sono resi conto che potrebbe essere utile considerare le cose da una prospettiva sperimentale. Ciò alla fine ha portato al loro recente studio.

"Nella dinamica del sistema aperto, gli errori perturbano il sistema e vorremmo conoscere la sensibilità del nostro esperimento a queste perturbazioni", ha detto Schuster. "Ciò suggerisce che la sensibilità di un esperimento agli errori deve essere correlata al modo in cui le informazioni si confondono. Basandosi su questa idea iniziale, abbiamo lavorato per rendere precisa la connessione tra errori e codifica e per analizzarne le conseguenze per i sistemi fisici e gli esperimenti di interesse. "

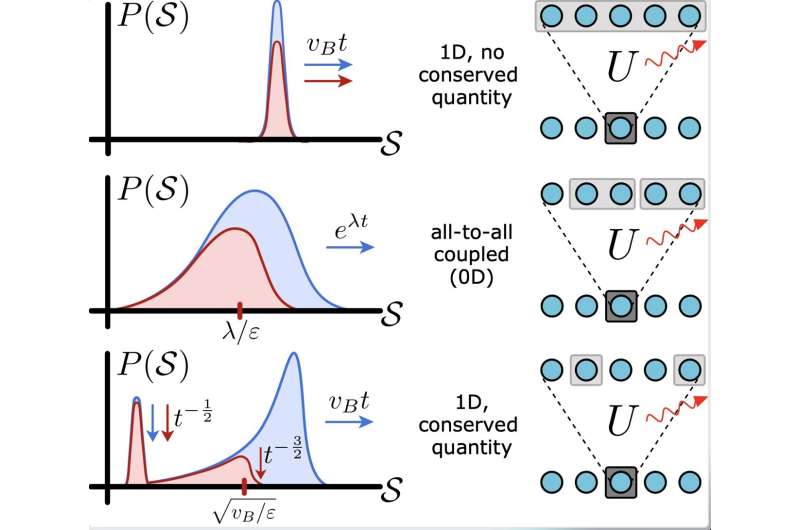
L’idea chiave alla base del recente studio di Schuster e Yao è che la codifica delle informazioni in un sistema aperto è in qualche modo indipendente dalla natura microscopica degli errori stessi. Piuttosto, tutto dipende da come questi errori influenzano le cosiddette "distribuzioni delle dimensioni dell'operatore", una caratterizzazione della complessità dell'operatore in base all'evoluzione nel tempo.

"La dinamica della distribuzione delle dimensioni degli operatori determina il modo in cui gli errori si diffondono in modo preciso", ha spiegato Schuster. "Al livello più semplice, questo assume la forma di due equazioni differenziali accoppiate. L'input delle equazioni è il modo in cui cambia la distribuzione delle dimensioni degli operatori, mentre l'output può essere considerato una previsione precisa di come si diffondono gli errori."

Sebbene alcuni studi precedenti avessero accennato a questo collegamento, nessuno finora lo aveva formulato in modo chiaro e preciso. In tal modo, Schuster e Yao hanno scoperto che l'interazione tra errori e codifica era molto più sfumata di quanto precedentemente previsto.

"Un altro risultato innovativo del nostro lavoro è che gli errori modificano anche il comportamento delle informazioni stesse," ha detto Schuster. "Ciò porta a un'interessante interazione tra errori e rimescolamento, descritta dalle equazioni menzionate sopra. Il risultato di questa interazione dipende dalla natura delle dinamiche stesse e può essere utilizzato come caratterizzazione intrinseca di queste dinamiche, oltre a prevedere varie proprietà di esperimenti."

Un contesto particolarmente fruttuoso per applicare la struttura di Schuster e Yao si presenta in alcuni esperimenti che coinvolgono la cosiddetta dinamica "ergodica" a molti corpi. Ciò potrebbe essere effettuato e validato in lavori futuri.

"Una piacevole sorpresa che abbiamo scoperto mentre completavamo i nostri risultati è che il nostro quadro si applica anche a un'ampia classe di esperimenti - chiamati 'eco di Loschmidt' - che hanno interessato le comunità della risonanza magnetica nucleare (NMR) e del caos quantistico". per diversi decenni", ha detto Schuster. "L'eco di Loschmidt è un esperimento mentale di termodinamica di lunga data, risalente a Josef Loschmidt e alla fondazione della termodinamica nel 1800."

Sebbene i metodi sperimentali relativi all'eco di Loschmidt abbiano continuato a migliorare, sia negli esperimenti di simulazione quantistica che negli studi sulla risonanza magnetica allo stato solido, l'interpretazione di questi segnali, in particolare per gli hamiltoniani interagenti in quest'ultimo contesto, ha continuato a essere impegnativa.

"Gli sperimentali adattavano varie forme funzionali (ad esempio, gaussiane o esponenziali o sigmoidi) ai loro dati, ma non avevano mai una spiegazione del motivo per cui un esperimento specifico seguiva una forma funzionale invece di un'altra", ha detto Schuster. "All'inizio degli anni 2000, i ricercatori hanno scoperto un quadro su come descrivere l'eco di Loschmidt nei sistemi quantistici a pochi corpi; tuttavia, il caso dei sistemi a molti corpi è rimasto una questione aperta. Crediamo che il nostro quadro possa fornire una risposta a questa domanda. domanda."

Oltre a far luce su come si propagano gli errori nei sistemi quantistici aperti a molti corpi, il recente lavoro suggerisce anche che i dati degli esperimenti sull'eco di Loschmidt potrebbero contenere più informazioni di quanto inizialmente sembri.

"L'interazione tra errori e dinamiche di distribuzione delle dimensioni degli operatori determina la forma funzionale dell'eco di Loschmidt", ha affermato Schuster. "Siamo fiduciosi che questo sia il caso dei modelli giocattolo che possiamo studiare numericamente e, nel lavoro futuro, speriamo di fornire un'analisi più dettagliata dei dati sperimentali dell'eco di Loschmidt per confermare che il nostro quadro si applica anche lì. Ce ne sono diversi indicazioni che lo suggeriscono fortemente, il che trovo piuttosto entusiasmante."

Guardando al futuro, Schuster e Yao sono interessati ad applicare la loro nuova struttura a una serie di altri esperimenti. Hanno inoltre in programma di esplorare le implicazioni dei loro risultati per la simulazione classica di sistemi quantistici aperti.

"Ci stiamo chiedendo se la nostra comprensione della diffusione delle informazioni in questi sistemi aperti possa effettivamente fornire informazioni su quanto vantaggio quantistico possa essere sfruttato da essi", afferma Yao. "E d'altra parte, è possibile progettare nuovi algoritmi per simulare in modo efficiente sistemi quantistici aperti."

Ulteriori informazioni: Thomas Schuster et al, Crescita degli operatori nei sistemi quantistici aperti, Lettere di revisione fisica (2023). DOI:10.1103/PhysRevLett.131.160402

Informazioni sul giornale: Lettere di revisione fisica

© 2023 Rete Scienza X