
Tarski dimostrò che un cerchio con raggio uno non può essere completamente coperto da strisce la cui larghezza combinata è inferiore a due:il diametro del cerchio. Ognuna delle strisce nell'immagine ha una lunghezza e un colore propri. Credito:MIPT
Israel Institute of Technology e Alexandr Polyanskii dell'Istituto di Fisica e Tecnologia di Mosca (MIPT) hanno dimostrato la congettura della zona di László Fejes Tóth. Formulato nel 1973, dice che se una sfera unitaria è completamente coperta da più zone, la loro larghezza combinata è almeno . La prova, pubblicato sulla rivista Analisi geometrica e funzionale , è importante per la geometria discreta e consente ai matematici di formulare nuovi problemi.
La geometria discreta studia le proprietà combinatorie dei punti, Linee, cerchi, poligoni e altri oggetti geometrici. Qual è il maggior numero di palline della stessa dimensione che possono stare intorno a un'altra palla della stessa dimensione? Qual è il modo più denso per imballare cerchi di dimensioni uguali su un aereo, o palline in uno spazio contenitivo? Queste e altre domande sono affrontate dalla geometria discreta.
Soluzioni a problemi come questi hanno applicazioni pratiche. Così, il problema dell'imballaggio denso ha aiutato a ottimizzare la codifica e correggere gli errori nella trasmissione dei dati. Un ulteriore esempio è il teorema dei quattro colori, che dice che quattro colori sono sufficienti per tracciare qualsiasi mappa su una sfera in modo che nessuna regione adiacente abbia lo stesso colore. Ha spinto i matematici a introdurre concetti importanti per la teoria dei grafi, che è cruciale per molti dei recenti sviluppi in chimica, biologia e informatica, così come i sistemi logistici.
La congettura della zona di Tóth è strettamente correlata a una serie di altri problemi di geometria discreta che sono stati risolti nel XX secolo quando si trattava di ricoprire una superficie con strisce. Il primo di questi è stato il cosiddetto problema della plancia, che consisteva nel ricoprire un disco con strisce delimitate da linee parallele. Alfred Tarski e Henryk Moese hanno offerto una semplice prova che mostra che la larghezza combinata di queste strisce, o tavole, non può superare il diametro del disco. Questo è, non c'è modo migliore per rivestire un disco che con un'unica tavola la cui larghezza è uguale al diametro del disco. Thøger Bang ha quindi risolto il problema coprendo un corpo convesso arbitrario con strisce. Vale a dire, ha dimostrato che la larghezza combinata delle strisce che coprono un corpo convesso è almeno la larghezza del corpo stesso, questo è, la larghezza minima di una singola striscia che copre il corpo.
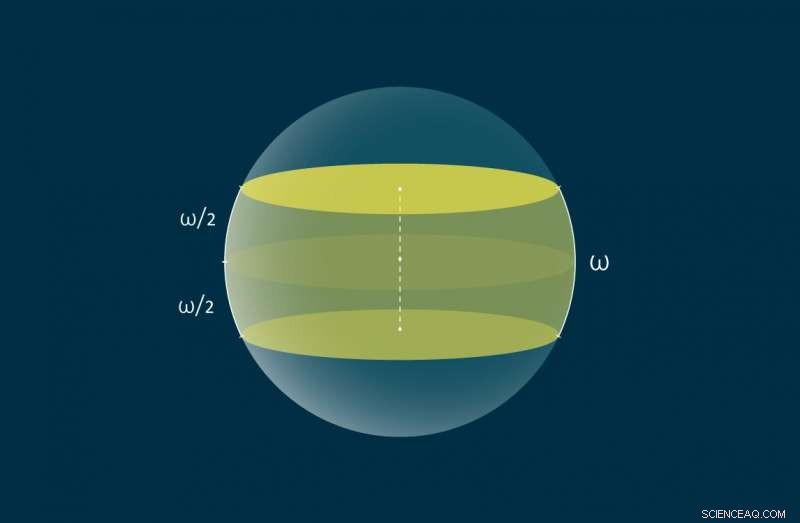
Una zona di larghezza sulla sfera è mostrata in giallo. Credito:MIPT
Il problema affrontato dagli autori è diverso in quanto riguarda la copertura di una sfera unitaria con zone appositamente costruite. Nello specifico, ogni zona è l'intersezione della sfera con una certa tavola tridimensionale, dove una tavola è la regione di spazio contenuta tra due piani paralleli simmetrici rispetto al centro della sfera. In alternativa, le zone possono essere definite nello spazio metrico geodetico senza ricorrere alle assi:una zona di larghezza sulla superficie di una sfera unitaria è l'insieme dei punti che si trovano a non più di /2 dal cerchio massimo, o equatore, con le distanze tra i punti misurate come gli archi più brevi che li collegano. I matematici dovevano trovare la larghezza minima combinata di tali zone che coprissero la sfera unitaria. Così, il problema differisce da quelli precedentemente risolti nel modo in cui viene misurata la larghezza:è definita come la lunghezza di un arco, piuttosto che la distanza euclidea tra rette o piani paralleli.
La prova presentata da Jiang e Polyanskii è stata ispirata da Bang, che ha risolto il problema della copertura di un corpo con strisce formando uno speciale insieme finito di punti all'interno del corpo, uno dei quali presumibilmente non era coperto da nessuna delle strisce. In un modo, sia Bang che gli autori producono una prova per assurdo. Nel caso della congettura di Fejes Tóth, i matematici ipotizzarono che la larghezza combinata delle zone che coprivano completamente la sfera fosse inferiore a e cercarono di arrivare a una contraddizione, vale a dire, trova un punto che giace sulla sfera ma non in nessuna delle zone.
Gli autori hanno dimostrato che è possibile formare un insieme di punti nello spazio tridimensionale in modo che almeno un punto non sia coperto dalle tavole che costituiscono le zone. Se tutto questo insieme si trova all'interno della sfera, è quindi relativamente facile tracciare un altro punto sulla sfera che non è anche coperto dalle tavole, e quindi dalle zone. Se uno qualsiasi dei punti dell'insieme si trova al di fuori della sfera, risulta possibile sostituire una zona più grande con più zone più piccole, la cui larghezza combinata è uguale a quella della zona più grande. Così, è possibile ridurre il numero di zone nel problema iniziale senza alterare la loro larghezza combinata. Infine, viene individuato un punto sulla sfera non coperto dalle zone. Ciò è contrario all'ipotesi che la larghezza combinata delle zone sia inferiore a , provando la congettura di Fejes Tóth.

Zone che coprono completamente una sfera. Ognuna delle cinque zone ha la propria larghezza e colore. Credito:MIPT
Il problema è stato risolto nello spazio n-dimensionale, ma gli autori dicono che questo non lo rende diverso dal caso delle tre dimensioni.
"Il problema di Fejes Tóth ha affascinato i matematici nel campo della geometria discreta per oltre 40 anni, " afferma l'autore Alexandr Polyanskii del Dipartimento di Matematica Discreta, MIPT. "Questo problema si è rivelato avere una soluzione elegante, che abbiamo avuto la fortuna di trovare. Il problema di Fejes Tóth ci ha spinto a considerarne un altro, congettura più fondamentale sulla copertura di una sfera da zone spostate definite come l'intersezione della sfera con assi tridimensionali che non sono necessariamente simmetriche centralmente".