
Figura 1:Espansione dei quartieri a partire dal nodo marrone al centro. Prima espansione:verde; secondo:giallo; terzo:rosso.
Una struttura grafica è estremamente utile per prevedere le proprietà dei suoi costituenti. Il modo più efficace per eseguire questa previsione è mappare ogni entità su un vettore attraverso l'uso di reti neurali profonde. Si può dedurre la somiglianza di due entità in base alla vicinanza del vettore. Una sfida per l'apprendimento profondo, però, è che è necessario raccogliere informazioni tra un'entità e il suo vicinato espanso attraverso i livelli della rete neurale. Il quartiere si espande rapidamente, rendendo il calcolo molto costoso. Per risolvere questa sfida, proponiamo un nuovo approccio, convalidato attraverso dimostrazioni matematiche e risultati sperimentali, ciò suggerisce che è sufficiente raccogliere le informazioni di solo una manciata di entità casuali in ogni espansione di quartiere. Questa sostanziale riduzione delle dimensioni del quartiere offre la stessa qualità di previsione delle reti neurali profonde all'avanguardia, ma riduce i costi di addestramento di ordini di grandezza (ad es. Da 10 a 100 volte meno tempo di calcolo e risorse), portando a una scalabilità accattivante. Il nostro articolo che descrive questo lavoro, "FastGCN:apprendimento rapido con reti convoluzionali di grafi tramite il campionamento dell'importanza, " sarà presentato a ICLR 2018. I miei coautori sono Tengfei Ma e Cao Xiao.
Complessità dell'analisi del grafico
I grafici sono rappresentazioni universali della relazione a coppie. Nelle applicazioni del mondo reale, vengono in una varietà di forme, includendo ad esempio social networks, reti di espressione genica, e grafici della conoscenza. Un argomento di tendenza nel deep learning è estendere il notevole successo di architetture di rete neurale consolidate per dati strutturati euclidei (come immagini e testi) a dati strutturati in modo irregolare, compresi i grafici. La rete convoluzionale del grafico, Rete Display di Google, è un esempio così eccellente. Generalizza il concetto di convoluzione per immagini, che può essere considerata una griglia di pixel, a grafici che non hanno più l'aspetto di una griglia regolare.
L'idea alla base di GCN è molto semplice. Quelli di noi che hanno seguito Signal Processing 101 o un corso base di visione artificiale hanno già familiarità con il concetto di filtro a convoluzione. Per le immagini, è una piccola matrice di numeri, da moltiplicare per elemento con una finestra in movimento dell'immagine, con la risultante somma del prodotto che sostituisce il numero centrale della finestra. Per i grafici, questo è simile. Una buona combinazione dei filtri può rilevare strutture locali primitive, come linee in angoli diversi, bordi, angoli, e macchie di un certo colore. Per i grafici, le circonvoluzioni sono simili. Immagina che ogni nodo del grafico sia inizialmente attaccato con un vettore. Per ogni nodo, in essa si sommano (con certi pesi e trasformazioni) i vettori dei vicini. Quindi, tutti i nodi vengono aggiornati contemporaneamente, eseguendo uno strato di propagazione in avanti. Le convoluzioni del grafo possono essere utilizzate per propagare le informazioni attraverso i quartieri in modo che l'informazione globale sia disseminata a ciascun nodo del grafo.
Il problema di GCN è che per una rete con più livelli, il quartiere si espande rapidamente, coinvolgendo molti vettori da sommare tra loro, anche per un solo nodo. Tale calcolo è proibitivo per i grafici con un gran numero di nodi. Quanto sarà grande un quartiere ampliato? Nell'analisi dei social network, esiste un famoso concetto coniato "sei gradi di separazione, " che afferma che si può raggiungere qualsiasi altra persona sulla Terra attraverso sei collegamenti intermedi! La figura 1 illustra che partendo dal nodo marrone al centro, espandendo il quartiere tre volte (nell'ordine del verde, giallo, e rosso) toccherà quasi tutto il grafico. In altre parole, aggiornare il vettore del solo nodo marrone è problematico per un GCN con solo tre strati.
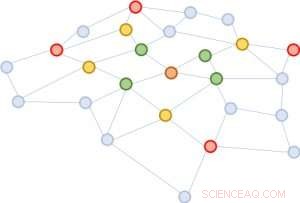
Figura 2:Partendo dallo stesso nodo marrone, in ogni espansione di quartiere, campioniamo solo quattro nodi.
Semplificare per la scalabilità
Proponiamo una soluzione semplice ma potente, chiamato FastGCN. Se espandere completamente il quartiere è costoso, perché non espandersi solo su pochi vicini ogni volta? La figura 2 illustra il concetto. Partendo dal nodo marrone, in ogni espansione scegliamo un numero costante (quattro) di nodi e sommiamo sui vettori solo da essi. Il campionamento riduce sostanzialmente il costo per l'addestramento della rete neurale, riducendo il tempo di formazione di ordini di grandezza su set di dati di riferimento comunemente usati dai ricercatori. Ancora, le previsioni rimangono relativamente accurate. La dimensione di questi grafici di riferimento varia da poche migliaia di nodi a poche centinaia di migliaia di nodi, confermando la scalabilità del nostro metodo.
Dietro questo approccio intuitivo c'è una teoria matematica per l'approssimazione della funzione di perdita. Uno strato della rete può essere riassunto come una moltiplicazione matriciale:H'=s(AHW), dove A è la matrice di adiacenza del grafico, ogni riga di H è il vettore attaccato ai nodi, W è una trasformazione lineare dei vettori (interpretata anche come parametro del modello da apprendere), e le righe di H' contengono i vettori aggiornati. Generalizziamo questa moltiplicazione matriciale in una trasformata integrale h'(v)=s(òA(v, u)h(u)W dP(u)) sotto una misura di probabilità P. Allora, il campionamento di un numero fisso di vicini in ogni espansione non è altro che un'approssimazione Monte Carlo dell'integrale sotto la misura P. L'approssimazione Monte Carlo fornisce uno stimatore consistente della funzione di perdita; quindi, prendendo il gradiente, possiamo usare un metodo di ottimizzazione standard (come la discesa del gradiente stocastico) per addestrare la rete neurale.
Una serie di applicazioni di deep learning
Il nostro approccio affronta una sfida chiave nel deep learning per grafici su larga scala. Si applica non solo a GCN ma anche a molte altre reti neurali a grafo costruite sul concetto di espansione di quartiere, una componente essenziale dell'apprendimento della rappresentazione grafica. Prevediamo che la risoluzione della sfida in questa struttura di dati fondamentale, i grafici, sarà adottata in una vasta gamma di applicazioni, compresa l'analisi dei social network, la profonda conoscenza delle interazioni proteina-proteina per la scoperta di farmaci, e la cura e la scoperta di informazioni nelle basi di conoscenza.