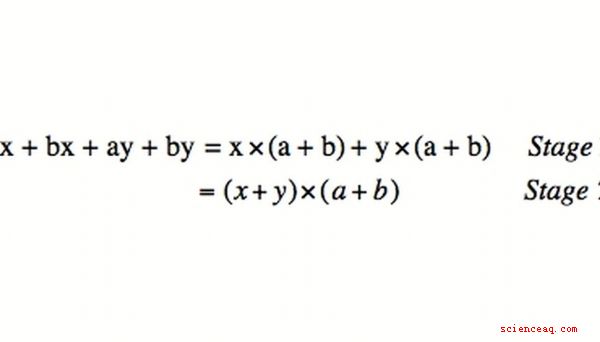
I quadratici sono polinomi di secondo ordine, cioè equazioni di variabili con esponenti che sommano al massimo 2. Ad esempio, x ^ 2 + 3x + 2 è un quadratico. Factoring significa trovare le sue radici, in modo che (x-root1) (x-root2) sia uguale al quadratico originale. Essere in grado di calcolare tale formula equivale a essere in grado di risolvere l'equazione x ^ 2 + 3x + 2 = 0, poiché le radici sono i valori di x dove il polinomio è uguale a zero.
Segni per il contrario Metodo FOIL
Il metodo FOIL inverso per quadrare il factoring pone la domanda: come si compila il modulo (? X +?) (? X +?) Quando si considera ax ^ 2 + bx + c (a, b, c costanti)? Ci sono alcune regole per il factoring che possono aiutare a rispondere a questo.
"FOIL" prende il nome dal suo metodo di moltiplicare i fattori. Per moltiplicare, diciamo, (2x + 3) e (4x + 5), 2 e 4 sono chiamati "primo", 3 e 5 sono chiamati "ultimo", 3 e 4 sono chiamati "interno" e 2 e 5 sono chiamati "esterno." La forma potrebbe quindi essere scritta come (FOx + LI) (FIx + LO).
Una regola di factoring utile per ax ^ 2 + bx + c è notare che se c > 0, allora LI e LO devono essere entrambi positivi o entrambi negativi. Allo stesso modo, se a è positivo, FO e FI devono essere entrambi positivi o entrambi negativi. Se c è negativo, allora LI o LO è negativo, ma non entrambi. Di nuovo, lo stesso vale per a, FO e FI.
Se a, c > 0, ma b < 0, allora la fattorizzazione deve essere fatta in modo che LI e LO siano entrambi negativi o FO e FI siano entrambi negativi. (Non importa quale, dal momento che entrambi i metodi porteranno a una fattorizzazione).
Regole per il factoring Quattro termini
Una regola per il factoring di quattro termini di variabili consiste nel tirare fuori termini comuni. Ad esempio, le coppie in xy-5y + 10-2x hanno termini comuni. Tirandoli fuori dà: y (x-5) + 2 (5-x). Nota la somiglianza di ciò che è tra parentesi. Pertanto, possono essere estratti anche: y (x-5) -2 (x-5) diventa (y-2) (x-5). Questo è chiamato "factoring per raggruppamento".
Estendere il raggruppamento alla quadratica
La regola per il factoring di quattro termini può essere estesa alla quadratica. La regola per farlo è: trovare i fattori di a --- c quella somma a b. Ad esempio, x ^ 2-10x + 24 ha un --- c = 24 eb = -10. 24 ha 6 e 4 come fattori, che aggiungono a 10. Questo ci dà un suggerimento sulla risposta finale che stiamo cercando: -6 e -4 si moltiplicano per dare 24, e si somma a b = -10.
Quindi ora la quadratica viene riscritta con b split up: x ^ 2-6x-4x + 24. Ora la formula può essere scomposta come quando si considera il raggruppamento, il primo passo è: x (x-6) + 4 (6-x).