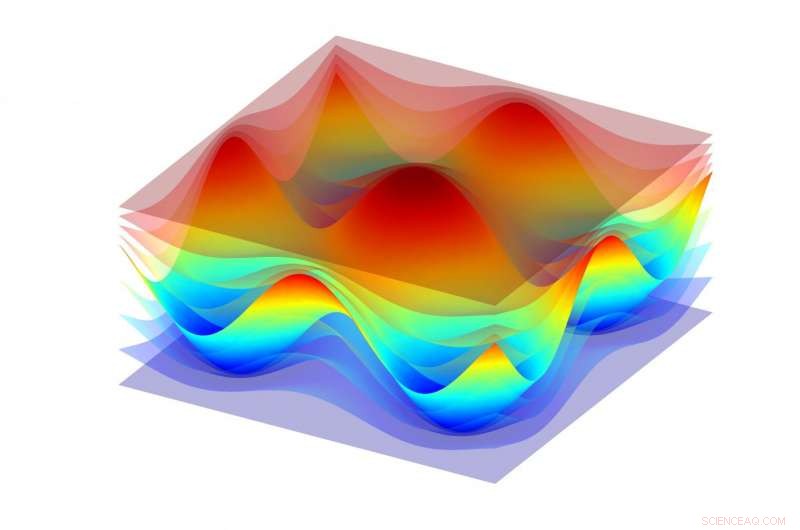
Piani di coordinate di un sistema di coordinate curvilineo introdotto in una regione vicino a un reticolo di diffrazione sinusoidale bidimensionale in modo che uno dei piani coincida con la superficie del reticolo (una superficie opaca). Credito:MIPT
I fisici del MIPT e dell'Università Jean Monnet (Francia) hanno sviluppato un nuovo metodo di simulazione per elementi ottici utilizzati in molti strumenti e dispositivi moderni. La loro carta, presentando una descrizione del metodo che consente di progettare dispositivi ottici complessi su schede grafiche da gioco, è stato pubblicato su Journal of Quantitative Spectroscopy and Radiative Transfer .
Alexey Shcherbakov, un dipendente del Laboratorio di Nanoottica e Plasmonica presso il Centro di Optoelettronica su Nanoscala del MIPT, e il suo collega dell'Università Jean Monnet Alexandre Tishchenko (1958-2016) hanno proposto un nuovo approccio al calcolo dei parametri ottici di reticoli di diffrazione complessi ed elementi di diffrazione. Le possibilità del metodo di nuova concezione sono significativamente maggiori di quelle offerte da altri metodi ampiamente utilizzati per una varietà di strutture ottiche. I risultati dello studio aprono nuove prospettive per l'ottimizzazione altamente efficiente dei moderni dispositivi ottici e optoelettronici.
I reticoli di diffrazione sono elementi ottici che costituiscono la base di molti dispositivi moderni in spettroscopia, telecomunicazioni e tecnologie laser. Sono strutture periodiche mono o bidimensionali contenenti migliaia di elementi regolari, ad es. una serie di strisce parallele di larghezza microscopica. I reticoli di diffrazione sono in grado di suddividere la luce bianca in uno spettro, riflettono raggi di lunghezze d'onda diverse in direzioni diverse:ecco perché vengono utilizzati praticamente in tutti gli spettrometri.
Un buon esempio di reticolo di diffrazione è un normale compact disc. Se è illuminato con luce a frequenza fissa, ad esempio un puntatore laser rosso, invece di un singolo raggio riflesso, appare una serie di raggi riflessi. Questi sono indicati come ordini di diffrazione. Le direzioni in cui si propagano questi fasci sono fisse e dipendono dal periodo del reticolo (definito come la distanza tra elementi adiacenti), l'angolo di incidenza, e la frequenza di radiazione. Calcolando l'intensità di ciascun ordine di diffrazione, cioè., la quantità di potenza della luce incidente che si riflette in ciascuna direzione, è molto più difficile. L'esecuzione di questo tipo di calcoli con elevata precisione è estremamente importante da un punto di vista pratico, poiché sono vitali per l'ottimizzazione di un'ampia varietà di strumenti e dispositivi.
La capacità dei reticoli di diffrazione di dividere la luce in uno spettro viene utilizzata negli spettrometri, dispositivi che utilizzano l'analisi dello spettro per determinare la composizione di varie sostanze, comprese soluzioni chimiche e gas interstellari. La simulazione della diffrazione è essenziale per la produzione di maschere per litografia utilizzate nella moderna fabbricazione microelettronica, e per la progettazione di polarizzatori speciali nella tecnologia di lavorazione laser dei metalli. Inoltre, strutture periodiche vengono utilizzate per aumentare l'efficienza dei concentratori solari e delle celle fotovoltaiche aumentando l'assorbimento della luce. Le strutture periodiche rendono anche più difficile falsificare documenti e denaro:un modello di sottili strisce metalliche su carta che riflettono la luce in un certo modo può fungere da contromisura per la falsificazione.
Un calcolo rigoroso dell'efficienza dell'ordine di diffrazione è possibile solo risolvendo le equazioni di Maxwell - equazioni fondamentali che descrivono il campo elettromagnetico e, in particolare, propagazione delle onde elettromagnetiche. Sono stati formulati più di cento anni fa, ma un'ampia varietà di soluzioni che queste equazioni ammettono in casi diversi motiva ancora molti scienziati in tutto il mondo a continuare a cercare nuove soluzioni. E descrivere complessi reticoli di diffrazione ottica usando le equazioni di Maxwell è possibile solo con l'aiuto di metodi numerici.

Alexey Shcherbakov dimostra il modello di diffrazione da un reticolo bidimensionale, credito:credito:MIPT
Ciò significa che invece di una formula pronta all'uso, deve essere implementato un algoritmo di precisione finita. Per analizzare e ottimizzare reticoli di diffrazione complessi, i ricercatori utilizzano computer moderni e cluster di computer. Un intero campo della scienza che combina la fisica matematica, analisi numerica, programmazione, e altre aree è dedicata all'esplorazione di come scrivere programmi per computer ed eseguire questi calcoli nel modo più efficiente. Lo sviluppo di questo campo è stimolato dai progressi nelle tecnologie di fabbricazione per le strutture di diffrazione. Dispositivi più precisi pongono requisiti sempre più elevati ai metodi di simulazione a livello di progettazione.
Nella loro pubblicazione, i ricercatori hanno sviluppato il Generalized Source Method (GSM), ha ridotto significativamente il consumo di risorse informatiche rispetto ad altri metodi. L'idea si basa su ipotetiche sorgenti di radiazione elettromagnetica che sostituiscono la disomogeneità strutturale.
Secondo Alexey Shcherbakov, un ricercatore senior del Laboratorio di Nanoottica, questa idea può, con alcune limitazioni, essere illustrato come segue:"Supponiamo di lanciare pietre nel centro di uno stagno circolare. Le onde generate dai sassi saranno circolari e si estenderanno dal centro dello stagno fino al bordo dell'acqua. Ora chiediamoci, che forma avranno le onde se una barca galleggia da qualche parte nello stagno? Si scopre che se rimuoviamo la barca e lanciamo molte piccole pietre nel punto in cui stava galleggiando, queste piccole pietre possono essere scelte in modo che il numero totale di onde generate da esse e il sasso che gettiamo al centro sia lo stesso come se la barca galleggiasse ancora nello stagno. Questa ipotetica sostituzione può sembrare complicare il compito, ma, in pratica, questo principio consente agli scienziati di risolvere in modo efficiente problemi molto complessi di propagazione delle onde".
L'idea chiave del nuovo metodo basato sul GSM era di utilizzare trasformazioni di coordinate curvilinee nella regione del reticolo. All'interno della logica del metodo, una superficie ruvida del reticolo è allungata su un piano, il che rende molto semplice calcolare la riflessione e la rifrazione delle onde. Preservare gli effetti fisici causati dalla rugosità richiede di modificare contemporaneamente le proprietà dell'ambiente vicino alla superficie in un certo modo su tale stiramento. Così, invece di riflettersi sulla superficie della griglia ondulata, le onde sembrano passare attraverso uno spazio disomogeneo, che rallenta la loro propagazione in modo diverso in luoghi diversi. Questa tecnica migliora notevolmente i calcoli ottenendo risultati molto più accurati nello stesso tempo di calcolo.
Oltre allo sviluppo analitico del nuovo approccio con fonti metriche, i ricercatori hanno anche dimostrato la possibilità di un'efficiente parallelizzazione del metodo e l'esecuzione di simulazioni su schede grafiche. Ciò significa che è possibile utilizzare componenti prodotti commercialmente con cui tutti i giocatori hanno familiarità per simulare reticoli di diffrazione molto complessi. La potenza di calcolo dei chip grafici è già maggiore della potenza dei processori, ecco perché le schede grafiche sono utilizzate in molti laboratori in tutto il mondo. Nella ricerca pubblicata, confrontando le simulazioni su schede grafiche e normali processori ha mostrato che un chip grafico è in grado di svolgere il compito decine di volte più velocemente.