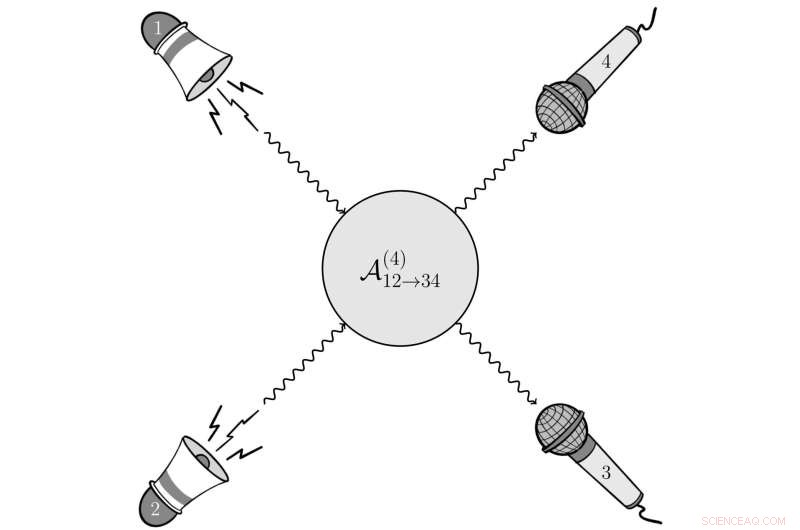
Vengono prodotte due onde sonore (1 e 2), che si disperdono in altre due onde sonore (3 e 4), che vengono poi rilevate. La probabilità di questo processo è descritta da un'ampiezza di scattering di 4 punti. Credito:Angelo Esposito
Non tutto ha bisogno di essere visto per essere creduto; certe cose si sentono più facilmente, come un treno che si avvicina alla sua stazione. In un recente articolo, pubblicato in Physical Review Letters , i ricercatori hanno messo le orecchie al binario, scoprendo una nuova proprietà di scattering ampiezze basata sul loro studio delle onde sonore attraverso la materia solida.
Che si tratti di luce o suono, i fisici considerano la probabilità delle interazioni delle particelle (sì, il suono può comportarsi come una particella) in termini di curve di probabilità o ampiezze di dispersione. È tradizione comune che quando la quantità di moto o l'energia di una delle particelle sparse va a zero, le ampiezze di scattering dovrebbero sempre scalare con potenze intere di quantità di moto (cioè, p 1 , p 2 , p 3 , eccetera.). Ciò che il team di ricerca ha scoperto, tuttavia, è che l'ampiezza può essere proporzionale a una potenza frazionaria (cioè, p 1/2 , p 1/3 , p 1/4 , ecc.).
Perché è importante? Sebbene le teorie dei campi quantistici, come il modello standard, consentano ai ricercatori di fare previsioni sulle interazioni delle particelle con estrema precisione, è ancora possibile migliorare le attuali basi della fisica fondamentale. Quando viene dimostrato un nuovo comportamento, come il ridimensionamento della potenza frazionaria, agli scienziati viene data l'opportunità di rivedere o rivedere le teorie esistenti.
Questo lavoro, condotto da Angelo Esposito (Institute for Advanced Study), Tomáš Brauner (Università di Stavanger) e Riccardo Penco (Carnegie Mellon University), considera in modo specifico le interazioni delle onde sonore nei solidi. Per visualizzare questo concetto, immagina un blocco di legno con altoparlanti posti su entrambe le estremità. Una volta che gli altoparlanti sono accesi, due onde sonore, i fononi, si incontrano e si disperdono, in modo simile alle collisioni in un acceleratore di particelle. Quando un altoparlante viene regolato a un certo limite, in modo tale che la quantità di moto del fonone sia zero, l'ampiezza risultante può essere proporzionale a una potenza frazionaria. Questo comportamento di ridimensionamento, spiega il team, non è probabilmente limitato ai fononi nei solidi e il suo riconoscimento può aiutare lo studio delle ampiezze di scattering in molti contesti diversi, dalla fisica delle particelle alla cosmologia.
"Le proprietà dettagliate delle ampiezze di scattering sono state recentemente studiate con molto vigore", ha affermato Esposito. "L'obiettivo di questo ampio programma è classificare i possibili modelli di comportamento delle ampiezze di scattering, sia per rendere alcuni dei nostri calcoli più efficienti, sia in modo più ambizioso, per costruire nuove basi della teoria quantistica dei campi."
I diagrammi di Feynman sono stati a lungo uno strumento indispensabile dei fisici delle particelle, ma presentano alcune limitazioni. Ad esempio, calcoli ad alta precisione possono richiedere l'inserimento di decine di migliaia di diagrammi di Feynman in un computer, per descrivere le interazioni delle particelle. Acquisendo una migliore comprensione delle ampiezze di scattering, i ricercatori potrebbero essere in grado di individuare più facilmente il comportamento delle particelle piuttosto che fare affidamento sull'approccio top-down dei diagrammi di Feynman, migliorando così l'efficienza dei calcoli.
"Il presente lavoro rivela una svolta nella storia, mostrando che la fisica della materia condensata mostra una fenomenologia molto più ricca di ampiezze di dispersione rispetto a quanto visto in precedenza nella fisica fondamentale e relativistica", ha aggiunto Esposito. "La scoperta del ridimensionamento della potenza frazionaria invita a ulteriori lavori sulla diffusione delle ampiezze delle oscillazioni collettive della materia, ponendo al centro i solidi". + Esplora ulteriormente