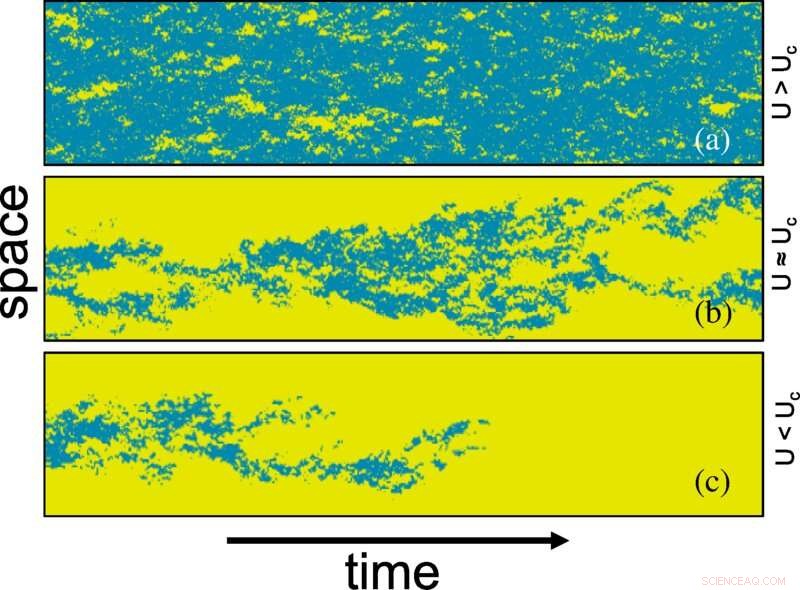
Grafico spazio-temporale della transizione laminare-turbolente in funzione di U (cioè il numero di Reynolds) generato dal modello PP nel flusso di Taylor-Couette quasi-1D. La turbolenza (in blu) è rappresentata dalla densità della preda B, generata dalla simulazione Monte Carlo su un reticolo 2D di dimensioni 20×3000 (a) al di sotto del punto critico U=0,0135 , (b) nel punto critico U=0,01425 e (c) al di sopra del punto critico U=0,0165. Il giallo rappresenta la fase laminare localmente non occupata dalla preda. La densità della preda è binarizzata a seconda che sia maggiore di 0,065 × densità massima della preda. Credito:Lettere di revisione fisica (2022). DOI:10.1103/PhysRevLett.129.034501
Menziona la parola "turbolenza" e potresti evocare immagini di voli accidentati, tempo tempestoso e correnti oceaniche o fluviali mosse. Per molti, la turbolenza è un fatto della vita quotidiana, ma è anche uno dei fenomeni fisici meno conosciuti. In particolare, il punto in cui il movimento di un fluido passa da un flusso regolare e prevedibile (noto come "laminare") a un flusso casuale e imprevedibile (noto come "turbolenza"), la cosiddetta transizione laminare-turbolente, continua a sconcertare gli scienziati da quando Osborne Reynolds lo studiò per la prima volta sperimentalmente nelle pipe nel 1883.
Ora, un team di scienziati con sede presso l'Università dell'Illinois Urbana-Champaign, l'Università della California a San Diego e l'Academia Sinica a Taiwan hanno mostrato come spiegare i modelli casuali e le dinamiche della turbolenza nei tubi nel regime di transizione. Il loro lavoro utilizza nuove idee che hanno origine in campi così disparati come la meccanica statistica e l'ecologia e si basa sulla crescente evidenza che la transizione laminare-turbolente ha proprietà statistiche che possono essere meglio pensate in termini di teoria delle transizioni di fase di non equilibrio.
Il team comprende lo studente laureato in fisica della UIUC Xueying Wang, il ricercatore dell'Accademia Sinica Hong-Yan Shih e la cattedra emerita di fisica dell'UIUC Swanlund e il professore di ricerca Nigel Goldenfeld. Goldenfeld è attualmente Distinguished Professor of Physics presso l'Università della California a San Diego.
Gli autori hanno pubblicato i loro risultati l'11 luglio 2022 sulla rivista Physical Review Letters .
Sbuffi e lumache sono caratteristiche della turbolenza di transizione
Reynolds ha scoperto che nei tubi, la transizione laminare-turbolente avviene in modo irregolare all'aumentare della velocità del flusso. Blocchi di fluido turbolento, noti oggi come "sbuffi", compaiono vicino alla transizione laminare-turbolente e sono separati da regioni di flusso laminare. I modi precisi in cui i soffi appaiono e si muovono o addirittura si dividono in due dipendono dalla geometria dello spazio attraverso il quale scorre un fluido. Questi complessi fenomeni contribuiscono alla meritata reputazione della turbolenza come uno degli ultimi problemi in sospeso nella fisica classica. A velocità ancora più elevate, le zone turbolente in realtà crescono piuttosto che spostarsi o dividersi:queste regioni in crescita di turbolenza sono chiamate "lumache".
Per costruire un quadro più chiaro della transizione alla turbolenza, i ricercatori hanno sviluppato un nuovo modello minimo per comprendere sbuffi e lumache utilizzando metodi importati dalla biologia teorica della popolazione. I ricercatori hanno scoperto che potrebbero rappresentare il flusso di energia del fluido vicino alla transizione laminare-turbolente in termini di flusso di energia che nasce in un ecosistema predatore-preda, in cui i nutrienti sono l'energia del flusso di fondo, il predatore è una certa struttura di flusso che inibisce la turbolenza, e la turbolenza è la preda. Questo modello ecologico riassume il comportamento turbolento sia nel tubo che nel flusso Taylor-Couette, un tipo di flusso rotazionale, un obiettivo che i modelli precedenti non erano riusciti a raggiungere.
Goldenfeld afferma:"Sei anni fa, è stata fatta una svolta con prove teoriche e sperimentali convergenti su una descrizione di sbuffi turbolenti che emergono dal flusso laminare, in termini di teoria della transizione di fase. Tuttavia, quel lavoro ha lasciato aperta la questione di cosa accada a flusso più elevato si allontana dal punto di non ritorno stesso.
"Il nostro nuovo lavoro mostra che la stessa struttura concettuale e gli stessi metodi si applicano anche nel regime dello slug e ricapitola in notevole dettaglio i risultati sperimentali. È fantastico vedere i concetti della teoria della transizione di fase e dell'ecologia si fondono nel problema completamente diverso della meccanica dei fluidi. "
Le lumache stesse mostrano comportamenti interessanti e sono disponibili in due versioni, lumache deboli e lumache forti, entrambe caratterizzate da almeno un "fronte", una regione contenente un confine tra fluidi laminari e turbolenti.
L'autore principale Wang spiega:"La parte anteriore di una lumaca è come un fronte meteorologico. Da un lato c'è il fluido laminare. Dall'altro lato c'è la turbolenza. Il fronte è come un confine di fase e si muove nello spazio a una velocità costante. velocità. Nei tubi si ottengono lumache oltre che sbuffi. Ma lumache deboli a velocità del fluido inferiori hanno un solo fronte a monte, mentre lumache forti a velocità più elevate hanno fronti sia a monte che a valle. Questi fattori e la ricchezza dei fenomeni di transizione rendono comprendere davvero la turbolenza di transizione. Il nostro lavoro fornisce una struttura unificata che gestisce tutti questi regimi, diverse geometrie di flusso e la casualità intrinseca."
I modelli predatore-preda e la turbolenza convergono
I ricercatori sono stati in grado di trarre vantaggio da una connessione sorprendente che avevano trovato in lavori precedenti tra biologia della popolazione e turbolenza di transizione.
Modellare il modo in cui i predatori interagiscono con le loro prede è un tema popolare nella biologia delle popolazioni. L'idea di base è semplice:i predatori si riproducono e mangiano le prede, riducendone la popolazione; anche le prede si riproducono, ripristinando il loro numero e fornendo cibo ai predatori. Quindi il ciclo si ripete. In poche parole, i predatori inibiscono la preda, mentre la preda rinforza i predatori. Gli scienziati possono dedurre molte informazioni da questi modelli, come il modo in cui le popolazioni di predatori e prede variano nel tempo, nonché il tempo impiegato da ciascuna per estinguersi a causa, ad esempio, di una mancanza di cibo o di un'eccessiva predazione.
In uno studio precedente, Shih e Goldenfeld, lavorando con l'ex studente universitario Tsung-Lin Hsieh (ora un borsista post-dottorato all'Università di Princeton), hanno mostrato che esiste un'analogia tra i modelli predatore-preda e la turbolenza che può essere espressa in termini matematici. Quando il fluido scorre attraverso un tubo, vengono generati due tipi di movimento del fluido. Il primo tipo è un modello a vortice che vortica attorno all'asse del tubo, chiamato "flusso zonale". Il secondo tipo è la turbolenza lungo l'asse del tubo. Gli autori hanno scoperto che la turbolenza si accumula costantemente e attiva il flusso zonale, che successivamente sopprime la turbolenza. In altre parole, il flusso zonale corrisponde ai predatori e la turbolenza corrisponde alla preda.
I ricercatori hanno scoperto che la distribuzione di probabilità della durata della turbolenza di transizione corrispondeva esattamente a quella di predatori e prede in un ecosistema, una connessione sorprendente considerando che la biologia della popolazione e la dinamica dei fluidi sono campi apparentemente disparati.
Hong-Yan Shih comments, "This connection helps us understand the complex transitional behavior of turbulence from the point of view of phase transitions in statistical mechanics. Specifically, this discovery provides the key ingredients to construct an effective theory, which leads to the prediction that the laminar-turbulent transition in fluids is a non-equilibrium phase transition in the directed percolation universality class.
"Directed percolation can be thought of as the familiar process that happens when water drips through coffee grounds in a percolator. If the grounds are too tightly packed, water can't get through. On the other hand, if the grounds are too loosely packed, water can get through but the coffee is undrinkable. There's a critical point where the water just manages to get through and takes long enough so that the coffee tastes good.
"Mathematically, that phenomenon is exactly what happens in the transition to turbulence and the transition of a functioning ecosystem. The mathematics of phase transitions, founded in the Nobel Prize–winning work of K. Wilson, explains how this remarkable phenomenon arises."
This prior work, however, looked at the turbulence of a single puff. Real life isn't as simple, and real fluids near the laminar-turbulent transition contain multiple puffs that grow, die out, and interact in complex ways as the flow speed increases. The researchers needed to extend their model to capture more complicated dynamics beyond those of a single puff.
Extending the predator-prey model by incorporating nutrients
To capture the complex dynamics found in experiments beyond the critical point in the current study, the authors decided to take into account energy balance in pipe flow.
Wang explains, "Turbulence is a dissipative structure that needs constant energy input to be sustained, and that energy comes from the laminar flow. This fact was previously shown by exact computer simulations of the fluid equations, but did not allow us to understand in a predictive way the phenomena that would emerge."
The researchers realized that, just like zonal flow and turbulence require energy to persist, predators and prey need nutrients from their environment to survive.
"We wanted to make a minimal model of the full energy balance to extend the previous work and capture energy extraction of turbulence from laminar mean flow," Wang adds. "So we introduced another component into the 'ecosystem':nutrients, which represent the kinetic energy of the mean flow."
The researchers numerically simulated the extended predator-prey model on a two-dimensional lattice having a length much larger than its width. They watched what happens when nutrients—that is, laminar state energy, from the fluid dynamics perspective—flow into the ecosystem, are consumed by the turbulence, and are restored downstream of the turbulence.
The model maps several pathways for energy and population dynamics. The first pathway takes input energy from the energy budget to turbulent energy, like prey extracting nutrients from their environment. A second pathway takes turbulent energy to zonal flow energy, like predators eating prey.
Once they established these predator-prey-inspired pathways, they sat back and watched computer simulations based on the new model, wherein energy entered the pipe and passed through the pathways randomly. Out of the randomness emerged features of transitional turbulence such as puffs, slugs, and their associated fronts, reproducing results seen in experiments. The simulations showed that the appearance of puffs or slugs—and whether slugs are of the weak or strong type—is determined by the input energy (or equivalently, the speed) of the fluid flow.
The researchers then successfully reproduced all the transitional phenomena observed in pipe flow experiments and explained the underlying physics of puff splitting and growth. Specifically, they found that puff splitting and interaction is highly probabilistic. As the fluid speed increases, the probability of puff splitting also increases. The puff-slug transition is gradual, and it occurs when puffs split so frequently that they start to fill up the system densely.
Rotational flow and new questions for turbulence
In addition to pipe flow, the researchers also simulated a special type of rotational flow known as Taylor-Couette flow in which a fluid moves in the space between two concentric cylinders and the outer cylinder rotates relative to the inner one. Unlike pipe flow, where the energy enters from the high-pressure end of the pipe, Taylor-Couette flow is sustained by shear, the stress that occurs when two boundaries move parallel to one another. The new model easily incorporated this difference and reproduced the patterns of transitional turbulence seen in experiments, demonstrating the flexibility of the model.
"We showed that the rich and complicated dynamical features in transitional pipe flow can be understood with a simple three-level stochastic predator-prey model based on energy balance in pipe flow," says Wang. "Our model also works for quasi-one-dimensional Taylor-Couette flow. Since energy balance generally holds in fluid systems, we expect our model to be applicable to systems with more complicated geometries as well."
Having described turbulence broadly by implementing their model in two different geometries, the team is already looking to answer new questions.
Goldenfeld says, "The next challenge is to see if and how our probabilistic model can be extended to two- or three-dimensional flows. This problem has been intensely studied for well over twenty years, with new experimental data starting to appear."
For his part, Goldenfeld is pleased to see diverse techniques converge to solve problems in complementary ways, a beautiful demonstration of how different fields of science can inform each other.
Goldenfeld summarizes, "Our results show how stochastic dynamics, pattern formation, phase transitions, and modeling concepts from diverse fields such as ecology can bring new tools, predictions, and insights into a problem previously considered within the more narrow disciplinary focus of fluid dynamics. It is exciting to see how successful minimal modeling is at capturing complex physical phenomena in a quantitative way." + Esplora ulteriormente