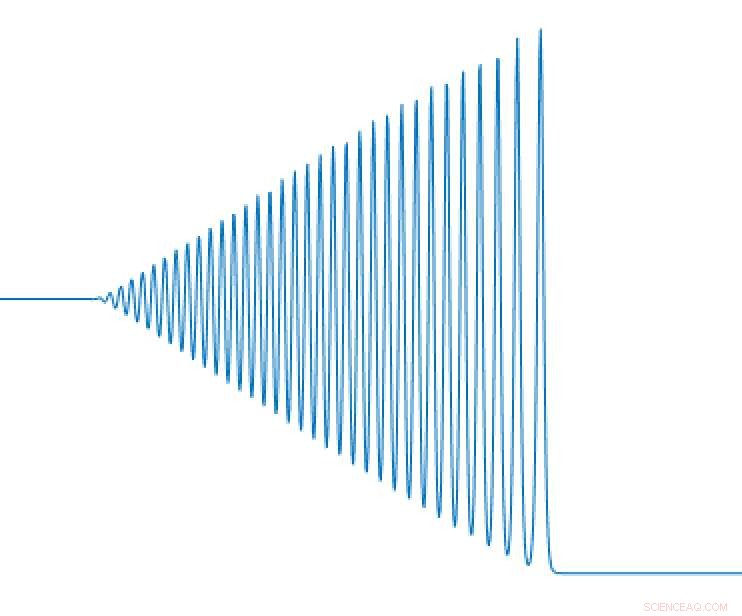
Diagramma schematico che mostra il tipico profilo dell'altezza del fluido attraverso un foro ondulato. Credito:Qiao Wang
Quando un fluido o un gas subisce un improvviso disturbo, come un cambiamento di pressione o elevazione, spesso dà origine a un fenomeno noto come foro ondulato, che consiste in una serie di rapide oscillazioni che si propagano e si diffondono.
In natura, questo spettacolo si verifica in molti contesti diversi, comprese onde d'acqua e plasmi, uno stato della materia costituito da gas ionizzati con particelle libere cariche positivamente e negativamente. Fenomeni simili si verificano anche nell'atmosfera.
Ma come descrivere ciò che traspare?
Un nuovo articolo di matematici dell'Università di Buffalo e dell'Università del Colorado Boulder ci avvicina alla ricerca di una risposta.
La ricerca, pubblicato ad agosto nel Atti della Royal Society A , presenta una serie di equazioni di nuova formulazione progettate per caratterizzare ciò che accade quando si verifica un foro ondulato e si diffonde lungo due assi. Visivamente, questo fenomeno assomiglia alle increspature concentriche che proliferano verso l'esterno quando si lancia un sasso in uno stagno.
"Vedi questi effetti nell'acqua, nei plasmi, nell'atmosfera, quindi le equazioni che descrivono queste onde emergono in un mucchio di campi diversi, "dice Gino Biondini, dottorato di ricerca, un professore di matematica presso l'UB College of Arts and Sciences. "Ci piace dire che la matematica è universale:la stessa matematica consente di descrivere molti scenari diversi".
I partner di Biondini nello studio erano Mark J. Ablowitz, dottorato di ricerca, professore di matematica applicata all'Università del Colorado Boulder, e Qiao Wang, Dottorando UB in matematica.
Un progresso nella matematica delle onde
Negli anni Sessanta, il matematico Gerald B. Whitham ha escogitato un approccio per descrivere i fori ondulati. Le equazioni da lui formulate potevano essere usate solo, però, quando un'onda viaggiava lungo un singolo asse (come un foro di marea che si propaga in una direzione lungo un canale stretto).
Il nuovo articolo di Ablowitz, Biondini e Wang si basano sulla teoria di Whitham derivando una serie di equazioni progettate per descrivere come tali increspature si formano e si propagano lungo due assi, in due possibili direzioni.
All'interno di questo quadro bidimensionale, il team ha già utilizzato le sue equazioni per studiare i fori ondulari la cui altezza d'onda varia solo lungo una delle due direzioni disponibili. Il prossimo passo nella ricerca è applicare le equazioni nella caratterizzazione dei fori ondulati la cui altezza d'onda cambia lungo entrambi gli assi.
"Le equazioni che abbiamo formulato segnano un passo avanti nella descrizione di questi interessanti fenomeni, " dice Biondini. "Inoltre, i metodi che abbiamo usato possono essere applicati per studiare una varietà di problemi fisici correlati, quindi speriamo che i nostri risultati possano aprire una lunga serie di lavori su questo tipo di argomenti".