Cosa significa per gli studenti se stanno imparando che la tecnologia può rispondere a ogni sfida?
I computer hanno aiutato la ricerca matematica ad accelerare in più direzioni e hanno aumentato la presenza della matematica nella vita di tutti i giorni.
Il ruolo della tecnologia nell'insegnamento e nell'apprendimento della matematica è sempre più nella mia mente come insegnante di matematica che vede arrivare nuovi studenti alla Simon Fraser University (SFU) ogni anno. Entrambi alla SFU, e quando visito le aule di matematica canadesi come oratore ospite, Guardo in stanze piene di giovani vivaci circondati da calcolatrici, computer e smartphone.
E va bene. Come molti matematici, Non ho resistito ai nuovi venti tecnologici introdotti dai tempi moderni. Ma tale tecnologia dovrebbe migliorare ed estendere, piuttosto che sostituire, la capacità di pensare matematicamente.
Addio geometria?
Recentemente, Ho incontrato un giovane interessato alla matematica e all'informatica, ma non sono sicuro in quale direzione vorrebbe andare. Ho proposto il seguente problema utilizzato dall'Università di Oxford per intervistare candidati universitari in matematica:"Immagina una scala appoggiata a una parete verticale con i piedi per terra. Il piolo centrale del la scala è stata dipinta di un colore diverso sul lato, in modo che possiamo vederlo quando guardiamo la scala dal lato in poi. Che forma traccia quel gradino centrale quando la scala cade a terra?"
Un modo per affrontare il puzzle della scala è usare, in modo relativamente semplice, geometria euclidea, per mostrare che la risposta è un quarto di cerchio. Vedi sotto:
Piuttosto che basarsi su proprietà geometriche, il giovane ha usato il linguaggio di programmazione Python per animare il problema e trovare la forma richiesta. Aveva imparato Python da solo all'inizio dell'estate. Quando gli ho chiesto dei triangoli congruenti, il giovane sembrava perplesso.
Situazioni come questa mi fanno temere che se non usate con la dovuta cura nelle aule, la tecnologia può privare gli studenti dello sviluppo completo delle loro abilità matematiche e spaziali.
Problemi irraggiungibili
Quello che i matematici chiamano "l'approccio computazionalmente assistito" ha permesso ai ricercatori di esplorare e risolvere problemi matematici che altrimenti sarebbero irraggiungibili. Mi viene in mente la dimostrazione assistita da computer del celebre Teorema dei Quattro Colori.
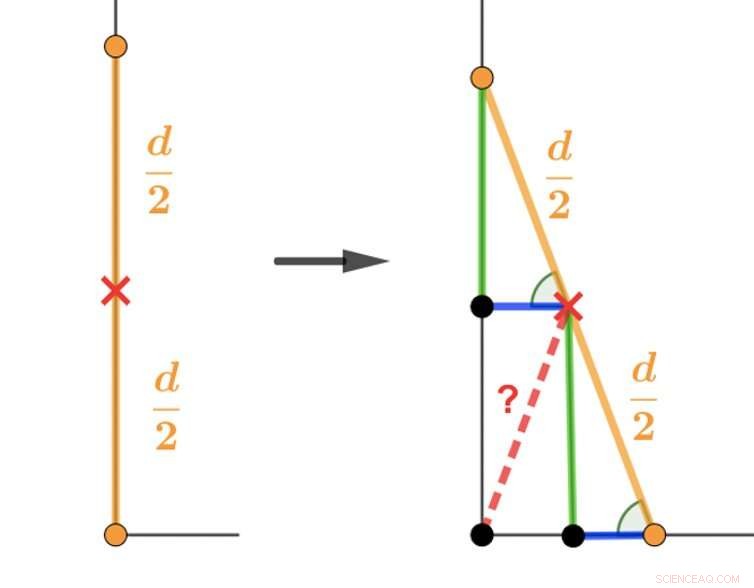
La geometria euclidea può essere utilizzata per risolvere il problema dato ai candidati universitari di matematica dell'Università di Oxford. Attestazione:Veselin, Autore fornito
Ma alcune domande matematiche hanno dimostrato i limiti della tecnologia esistente e il fatto che alcune soluzioni dipendono in gran parte dall'intuizione umana, ispirazione e intelligenza. Uno di questi problemi, noto come il problema del partito (sì, come in una cena), è trovare il numero di ospiti che garantirebbe che si possano sempre trovare sei persone che sono amici in comune o sei persone che sono reciprocamente sconosciute.
In termini matematici, questo problema riguarda il trovare quello che viene chiamato "il numero di Ramsey R(6, 6), " relativo a una branca della matematica che studia quali condizioni devono esistere affinché un dato modello appaia.
Credici o no, dal 1930 i matematici sanno che R(6, 6) esiste; dal 1994 sappiamo che questo numero è compreso tra 102 e 165.
Nessun progresso da allora!
Matematica sperimentale
I celebri matematici e fratelli canadesi Peter Borwein e Jonathan Borwein, che nel 1993 hanno fondato il Center for Experimental and Constructive Mathematics alla SFU, sono stati tra i pionieri della ricerca che hanno contribuito al processo di allineamento della matematica e delle nuove tecnologie.
Come suggerito da Jonathan Borwein e dal matematico David H. Bailey, la matematica sperimentale utilizza "un approccio computazionalmente assistito alla ricerca matematica". Significavano che la matematica sperimentale riguarda l'uso dei computer per potenziare i processi che sono stati gli elementi di base della ricerca matematica per secoli:
Hanno anche sostenuto che i computer potrebbero aiutare con l'esecuzione di lunghe derivazioni matematiche e la conferma dei risultati derivati analiticamente.
Il loro punto era che i computer consentono ai ricercatori di spingere le loro esplorazioni in dimensioni nuove o diverse.
Nuova esplorazione
Le idee di Bailey e Borwein possono essere utilizzate per descrivere i modi contemporanei e futuri di insegnare la matematica per aiutare gli studenti a guardare i problemi in modi nuovi.
Nel mio aneddoto Geometria-Pitone, Avrei potuto sfidare lo studente osservando che la forma ottenuta dall'animazione generata da Python sembra solo un quarto di cerchio (questo può riferirsi ai punti 1-3 e 5 nella definizione di Bailey-Borwein) e che una risposta completa richiederebbe un risultato analiticamente derivato (punto 6).
Per giustificare la sfida, Potrei anche scegliere di mostrare allo studente una prova visiva apparentemente strabiliante, come l'animazione che "mostra" 64 =65.
Potrei concludere citando il matematico e filosofo del XVII secolo René Descartes, che decise:"... di non accettare mai per vero nulla che io non sapessi chiaramente essere tale; vale a dire, attentamente... evitare... pregiudizi, e di non comprendere nient'altro nel mio giudizio di ciò che è stato presentato alla mia mente in modo così chiaro e distinto da escludere ogni motivo di dubbio".
Curricula di matematica sperimentale
Ricercatori ed educatori hanno sviluppato programmi di studio specializzati nell'insegnamento a bambini e giovani come utilizzare i computer per migliorare ed estendere il proprio apprendimento e pensiero matematico nelle scuole superiori canadesi. Per esempio, Il Progetto Curriculum RabbitMath, guidato dal matematico Peter Taylor della Queen's University e Chris Suurtamm dell'Università di Ottawa, o il Progetto Callysto, sostenuto dal Pacific Institute for Mathematical Sciences (PIMS) e dall'organizzazione no-profit Cybera con sede in Alberta.
La sfida per la comunità degli insegnanti di matematica riguarderà sempre più la creazione e il mantenimento di un sano equilibrio nelle nostre classi tra il potere del rigoroso, matematica formale e la potenza del calcolo.
Quando penso al futuro, Sono preoccupato che le parti rigorose e formali della matematica possano svanire ed essere lasciate fuori dalla portata degli studenti.
Per uno studente in un futuro non troppo lontano, voluto, Per esempio, il numero pi diventa un numero razionale, il che significa, sarebbe uguale alla sua approssimazione generata dal computer più potente al momento?
Più importante, cosa significherà tutto questo per gli studenti e per il loro apprendimento della matematica come strumento per navigare meglio nel mondo che li circonda?
Questo articolo è stato ripubblicato da The Conversation con una licenza Creative Commons. Leggi l'articolo originale. 