
Origami computazionali di reverse engineering per il confezionamento conforme. (A) Le rughe si formano quando si avvolge strettamente un foglio di carta rettangolare attorno a una superficie gaussiana diversa da zero. (B) I modelli di taglio frattale possono evitare le rughe ma inevitabilmente portano ad aperture e aree scoperte. (C) Lo sviluppo 2D di un poliedro sferico generato automaticamente da un origami computazionale può avvolgere una sfera d'acciaio senza lasciare aree scoperte. (D) All'aumentare del numero di sfaccettature, la morbidezza e la conformabilità della rete migliorano naturalmente. La differenza di superficie tra la sfera perfetta e il poliedro approssimato diminuisce del 5,3% quando il numero di sfaccettature aumenta da 80 a 500. Anche la distanza di Hausdorff tra le superfici poliedriche e la sfera perfetta si riduce dal 7,05 all'1,17% del raggio di la sfera perfetta quando il numero di sfaccettature aumenta da 80 a 500 (Photo credit:Y.-K. Lee, Università Nazionale di Seul). Credito:progressi scientifici, doi:10.1126/sciadv.aax6212
La domanda controintuitiva su come avvolgere una superficie sferica curva utilizzando materiali convenzionalmente rigidi e non estensibili o fragili, costituisce la base di questo studio. Per rispondere alla domanda, Yu-Ki Lee e un team di ricerca nei dipartimenti di ingegneria dei materiali e informatica nella Repubblica di Corea e negli Stati Uniti hanno esteso un metodo di progettazione geometrica di origami computazionali per avvolgere costrutti sferici in un nuovo rapporto ora pubblicato in Progressi scientifici . L'approccio ha fornito un metodo robusto e affidabile per progettare dispositivi conformi per superfici curve arbitrarie utilizzando una rete sviluppabile non poliedrica progettata computazionalmente. La progettazione assistita da computer ha trasformato materiali bidimensionali (2D) come wafer di silicio (Si) e lamiere di acciaio in strutture conformi che potrebbero avvolgere completamente strutture 3D senza fratture o deformazioni. Il metodo di avvolgimento computazionale ha permesso loro di sviluppare una piattaforma di progettazione per trasformare dispositivi 2-D convenzionalmente non estensibili in superfici curve 3-D conformi.
Lo studio ha introdotto un metodo universale per i materiali convenzionali non estensibili per avvolgere superfici curve 3-D arbitrarie e diverse progettando dispositivi di materiale conforme senza sacrificare le loro prestazioni. Per esempio, avvolgere una sfera con un pezzo di carta rettangolare può inevitabilmente formare delle rughe, mentre il tentativo di avvolgere una sfera con un substrato più duro può causare la rottura del materiale di avvolgimento. Per facilitare il processo, gli scienziati dei materiali possono introdurre tagli modellati nei materiali non estensibili, inclusi modelli di taglio reticolare e modelli di taglio frattale per avvolgere efficacemente le superfici 3D. Tali concetti sono programmabili in forma e possono coprire efficacemente una sfera. Gli ingegneri hanno anche consigliato algoritmi informatici per progettare modelli 3-D complessi basati su strutture auxetiche 2-D. Per ottenere una copertura ottimale, hanno introdotto una strategia di progettazione computazionale nota come "avvolgimento computazionale con reti sviluppabili non poliedriche, " per formare piattaforme di materiale non estensibile per dispositivi indossabili e conformi.
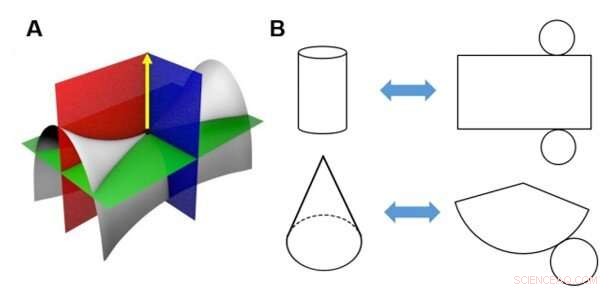
Limitazione matematica dell'avvolgimento di un foglio planare attorno a una superficie 3D con curvature gaussiane diverse da zero. (A) La curvatura gaussiana è il prodotto vettoriale delle curvature principali massima e minima in un punto. Al punto di sella (punto nero) della superficie grigia, una delle curvature principali è l'intersezione tra le superfici rossa e grigia, e l'altro è l'intersezione tra le superfici blu e grigie. Entrambi i piani rosso e blu contengono il vettore normale del punto di sella, e le loro intersezioni con la superficie grigia definiscono le curvature principali. Un materiale 2D con zero punti di curvatura gaussiana, come un foglio di carta, si chiama “superficie sviluppabile”, che non può essere trasformato in una superficie 3D con una curvatura gaussiana positiva o negativa (cioè, una “superficie non sviluppabile”) senza allungarsi o comprimersi. (B) Ad esempio, un cilindro o un cono possono essere coperti con carta tagliata, ma una sella o una sfera non possono essere avvolte senza la formazione di rughe o tagli. Anche il processo inverso (appiattimento) è lo stesso, ecco perché ci sono distorsioni nella mappa planare della Terra. Credito:progressi scientifici, doi:10.1126/sciadv.aax6212
In teoria, i ricercatori possono caratterizzare una superficie curva dalla curvatura gaussiana, che è il prodotto vettoriale delle curvature principali massima e minima in un punto. Per esempio, un foglio di carta è chiamato "superficie sviluppabile" e rappresenta un materiale 2-D con curvatura gaussiana zero in tutti i punti. Una superficie sviluppabile non può essere trasformata in una superficie 3D non sviluppabile senza strappi, allungando o comprimendo il materiale. Il concetto è matematicamente dimostrato dal "Teorema di Gauss Egregium, " che afferma che "Per spostare una superficie su un'altra superficie, la curvatura gaussiana di tutti i punti corrispondenti deve corrispondere". Net. I recenti metodi di calcolo mirano a ottimizzare la qualità e la piegabilità della rete utilizzando metodi di apprendimento automatico al fine di ridurre il tempo e lo sforzo richiesti per gli approcci tradizionali per tentativi ed errori.
Poiché la maggior parte degli oggetti 3D del mondo reale sono lisci e curvi, gli scienziati richiedono mesh ad alta risoluzione per coprire accuratamente le superfici. In questo lavoro, Lee et al. ha sviluppato un nuovo approccio noto come "avvolgimento computazionale" che va oltre il metodo di piegatura computazionale convenzionale. Per realizzare questo, hanno considerato la progettazione conforme del dispositivo come un problema di avvolgimento della carta anziché una sfida di piegatura della carta (origami). Il team ha riconosciuto le funzioni di attaccare e avvolgere dispositivi conformi per coprire una superficie 3D curva sottostante, semplicemente piegando e pressando una rete poliedrica senza pieghe.

Concetto e dimostrazione fisica del wrapping computazionale. (A) Quando la somma degli angoli di piegatura di una rete è ridotta al minimo, le linee di piega possono essere ignorate per accogliere materiali rigidi e fragili flessibili ma non elastici. Per 500 maglie, gli spazi vuoti nel caso di un materiale rigido e le pieghe nel caso di un materiale flessibile non sono più visibili, e la differenza tra i due diventa impercettibile. (B) Un foglio di acciaio inossidabile non estensibile viene tagliato in una rete sviluppabile. (C) Con un numero sufficiente di maglie, la lamiera di acciaio inossidabile può essere piegata e avvolgere completamente una sfera senza pieghe o pieghe. (D) Parte della sfera è spiegata con 400 maglie, e le linee di piega vengono rimosse. (E) Un wafer di Si fragile spesso 20 μm viene tagliato in una rete spiegata con un laser cutter. (F) Il wafer di Si tagliato avvolge stabilmente sia i telai convessi che quelli concavi. (Credito fotografico:Y.-K. Lee, Università Nazionale di Seul). Credito:progressi scientifici, doi:10.1126/sciadv.aax6212
Le mesh ad alta risoluzione hanno permesso loro di affrontare i limiti dei lunghi tempi di fabbricazione e dell'affidabilità meccanica. Per racchiudere una superficie con curvatura gaussiana totale diversa da zero, come una sfera perfetta, Lee et al. utilizzato una superficie sviluppabile dopo aver rifinito la mesh di sfaccettatura per soddisfare i valori richiesti di tenuta dell'avvolgimento. I risultati hanno fornito dati su una rete sviluppabile non poliedrica per creare spazi controllati e vincolati tra la rete e la sfera senza spazi o sovrapposizioni tra le sfaccettature. Il processo di fabbricazione ha prodotto con precisione superfici 3D altamente complesse e lisce molte volte più velocemente rispetto ai metodi di piegatura computazionale convenzionali quando si maneggiano forme complesse utilizzando la carta, materiali di rivestimento metallici e ceramici. L'analisi degli elementi finiti ha confermato che tali involucri computazionali erano meccanicamente affidabili.

Simulazione agli elementi finiti (FE) per avvolgere una sfera con un wafer di Si di 100 µm di spessore con una rete sviluppabile non poliedrica. Credito:progressi scientifici, doi:10.1126/sciadv.aax6212
Le strutture sviluppate nel lavoro hanno portato a un aumento significativo degli origami computazionali per i processi di fabbricazione industriale del mondo reale. Per esempio, Lee et al. sviluppato un dispositivo conforme utilizzando pannelli di lampade elettroluminescenti (EL) per avvolgere una sfera, il dispositivo conforme 3-D risultante ha mostrato una buona funzione e hanno attribuito i risultati ai processi di piegatura e pressatura utilizzati per avvolgere la sfera invece delle tecniche di cordonatura e piegatura. Il team ha anche dimostrato in modo simile il loro metodo su una maschera coreana commerciale e su un veicolo giocattolo elettrico con pannelli EL collegati per funzionare senza guasti. Generare la rete sviluppabile per componenti con superficie gaussiana diversa da zero come i fari del veicolo elettrico giocattolo, gli scienziati hanno utilizzato il metodo di spiegamento dell'algoritmo genetico (GA).

Dimostrazione di dispositivi conformi. (A) Tagliabile, non estensibile, i pannelli EL commerciali costituiti da elettrodi fragili vengono tagliati con un laser cutter per formare reti sviluppabili per una sfera. (B) I pannelli EL con una rete sviluppabile possono coprire completamente una sfera e (C) funzionare senza guasti catastrofici. (D ed E) Il concetto di avvolgimento computazionale è dimostrato anche per un modello ellissoide. (F e G) Oltre a una sfera e un ellissoide, una maschera facciale coreana commerciale può anche essere adeguatamente coperta con pannelli EL e azionata senza guasti elettrici. (H) Un veicolo giocattolo elettrico può anche essere avvolto in modo conforme con pannelli EL allo stesso modo, e anche i pannelli EL collegati funzionano bene senza guasti. Il metodo di sviluppo GA viene utilizzato per generare la rete sviluppabile per parti con superfici gaussiane diverse da zero, inclusi (I) i fari, il bordo del paraurti anteriore, e (J) il bordo del paraurti laterale posteriore del veicolo giocattolo elettrico. (Credito fotografico:Y.-K. Lee, Seoul National University.) Credito:progressi scientifici, doi:10.1126/sciadv.aax6212
In questo modo, Yu-Ki Lee e colleghi hanno introdotto il concetto di avvolgimento computazionale per convertire dispositivi flessibili 2-D non estensibili in dispositivi conformi 3-D. Utilizzando il metodo, racchiudevano una superficie con curvatura gaussiana diversa da zero come una sfera perfetta. La tecnica proposta potrebbe controllare la distanza tra le due superfici per garantire un avvolgimento stretto. Il lavoro ha prodotto un'unica superficie connessa nota come rete sviluppabile non poliedrica, progettato per avvolgere in modo conforme un foglio 2D per qualsiasi superficie 3D. Di conseguenza, gli scienziati sono stati persino in grado di facilitare materiali rigidi e fragili come fogli di metallo e wafer di silicio per coprire e avvolgere completamente superfici con curvatura gaussiana diversa da zero. Il metodo di avvolgimento computazionale universale sviluppato in questo lavoro fornirà nuove informazioni sullo sviluppo di dispositivi conformi con forme arbitrarie utilizzando algoritmi efficienti e robusti, metodi di fabbricazione affidabili.
© 2020 Scienza X Rete