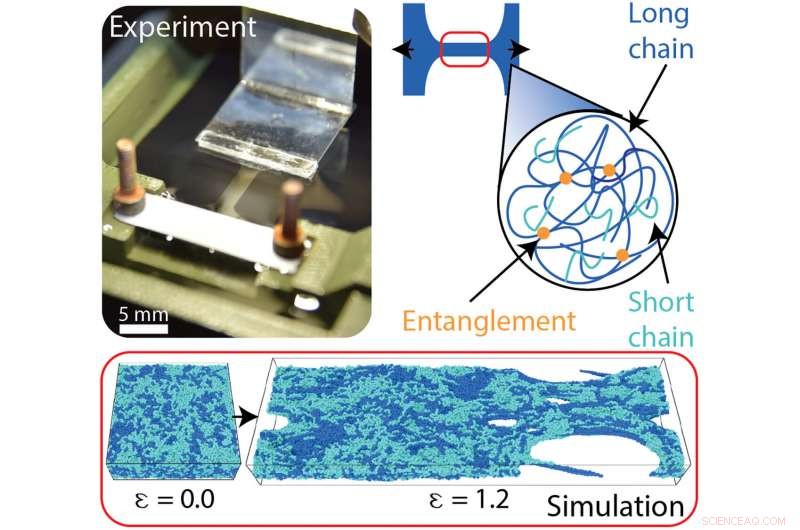
Film sottili omopolimerici misti. Esemplare macroscopico sperimentale a forma di osso di cane (nella foto) caricato in TUTTUT per estensione uniassiale. Le simulazioni a livello molecolare mostrano catene che scorrono l'una sull'altra per formare aperture nel film mentre viene teso. I sistemi misti sono composti da catene lunghe (blu scuro) e corte (azzurro chiaro) in cui la maggior parte degli intrecci portanti (punti arancioni), se non tutto, sono tra le lunghe catene polimeriche. Credito fotografico:C. Bukowski, Università del Massachusetts Amherst. Credito: Progressi scientifici , 10.1126/sciadv.abg9763
Il ruolo degli entanglement può determinare le proprietà meccaniche delle miscele di polimeri di vetro. In un nuovo rapporto ora pubblicato su Progressi scientifici , Cynthia Bukowski e un gruppo di ricerca in scienza dei polimeri e ingegneria biomolecolare presso l'Università del Massachusetts e l'Università della Pennsylvania, NOI., ha sviluppato un metodo combinato di esperimenti e simulazioni per quantificare il ruolo degli entanglement sui vetri polimerici. Il team ha condotto esperimenti di estensione uniassiale su film sottili da 100 nm con una miscela bidispersiva di polistirene, per il confronto con simulazioni di dinamica molecolare di un modello a grana grossa di vetri polimerici. Le miscele bidispersive hanno consentito la messa a punto sistematica della densità di entanglement presente in entrambi i sistemi e gli scienziati hanno misurato sperimentalmente la resistenza del film e descritto la tenacità del film simulata utilizzando un modello per tenere conto degli entanglement portanti.
Rottura di polimeri vetrosi
I polimeri vetrosi sono importanti per una vasta gamma di tecnologie, dalla produzione additiva alle membrane per la filtrazione dell'acqua pulita. La rigidità e la lavorabilità dei materiali li rendono interessanti per molte applicazioni per i ricercatori per determinarne la durata e i limiti di prestazione. Gli intrecci tra le molecole polimeriche allo stato vetroso svolgono un ruolo significativo per determinare la forza. I materiali polimerici vetrosi sono eccessivamente fragili al di sotto di un numero critico di entanglement per molecola e possono rompersi a livelli di stress decrescenti. I materiali polimerici possono dissipare energia al di sopra di una densità di entanglement critica per migliorare la loro forza e tenacità. Questi processi sono unici e danno origine a tecnologie ad ampio raggio. Gli ingrandimenti sono importanti per la resistenza ma richiedono solventi volatili e costosi o temperature eccessive durante la lavorazione. In questo lavoro, Bukowsky et al. ha combinato nuove strategie sperimentali con simulazioni di dinamica molecolare per rivelare come tutti gli entanglement non contribuissero allo stesso modo a un vetro polimerico. Il team ha sviluppato e convalidato una teoria di ridimensionamento per descrivere il numero di intrecci di rinforzo per catena polimerica per fornire una struttura per massimizzare la resistenza con intrecci minimi in un vetro polimerico.
Comportamento sforzo-deformazione delle miscele polimeriche. (A) Risposta sollecitazione-deformazione di deformazione uniassiale rappresentativa per ciascuna miscela testata sperimentalmente su TUTTUT. rappresenta la frazione di volume delle lunghe catene nel sistema. Il grafico in alto mostra le miscele con 13,7 kDa come diluente a catena corta e quello in basso con 59,5 kDa. (B) Risposte sforzo-deformazione di deformazione uniassiale di N =250 (⟨Z⟩ =15,9) miscelate con N =30 (in alto) e 60 (in basso) a una temperatura di T/Tg =0,71. ⟨Z⟩ è 1,8 e 3,6 per ogni catena corta, rispettivamente. La risposta a bassa deformazione è inclusa nell'inserto di ogni sezione. (C) Il modulo elastico (E) per ogni miscela misurata sperimentalmente. (D) La sollecitazione massima media per ciascuna miscela misurata sperimentalmente. Le barre di errore sono 1 SD da cinque a nove film in media. I simboli aperti rappresentano miscele che sono state tentate ma troppo fragili per essere manipolate in TUTTUT e allungate uniassialmente. (E) Il modulo elastico per ogni miscela simulata. (F) Il valore di tenacità per ciascuna miscela simulata. Credito: Progressi scientifici , 10.1126/sciadv.abg9763 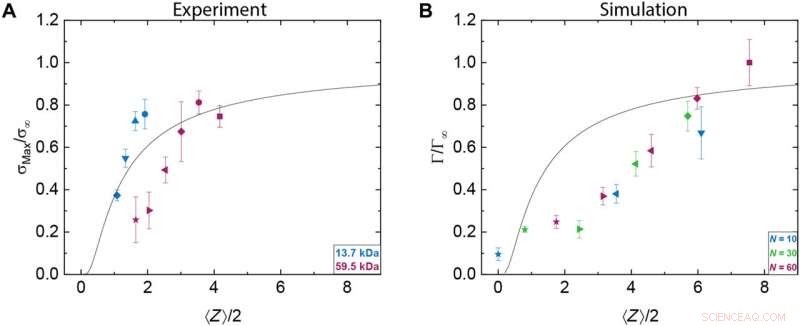
Le proprietà meccaniche dei vetri polimerici dipendevano dall'interazione delle forze e degli intrecci di van der Waals. La deformazione plastica è spesso associata a zone di deformazione a taglio che precedono la crescita della cricca. Gli entanglement svolgono un ruolo significativo nelle zone di deformazione da taglio e la loro stabilità o resistenza alla formazione di cricche è una funzione della densità di entanglement, nonché della temperatura e della velocità di deformazione. Queste deformazioni possono essere monitorate sperimentalmente con microscopia ottica ed elettronica a trasmissione. Bukowsky et al. ha superato i limiti esistenti dello studio utilizzando un metodo sperimentale di recente sviluppo per misurare la risposta sforzo-deformazione di film polimerici ultrasottili. Le simulazioni di dinamica molecolare (MD) hanno fornito preziose informazioni sul processo di entanglement nelle fusioni polimeriche e nei vetri, dove le simulazioni concordavano molto bene con gli esperimenti. Oltre alle simulazioni, le teorie dello scaling hanno anche contribuito a definire il ruolo degli entanglement nelle proprietà meccaniche dei vetri polimerici. L'approccio combinato di approcci sperimentali e MD ha permesso al team di esaminare la prospettiva macroscopica dei film sperimentali e la vista molecolare delle simulazioni dinamiche locali, per capire la forza del polimero.

Dati tracciati rispetto al modello Mikos e Peppas. Sollecitazione massima sperimentale normalizzata, Max/σ∞ (A), e tenacità simulata normalizzata, /Γ∞ (B), in funzione degli intrecci, Z⟩. Qui, ⟨Z⟩ è il Mn ottenuto dalla cromatografia a permeazione di gel di ciascuna miscela diviso per il Me del polistirene (18,1 kDa). Per le simulazioni, ⟨Z⟩ è la lunghezza media della catena N per ciascuna miscela divisa per Ne (16). Lo stress massimo e la tenacità sono normalizzati dallo stress massimo delle catene di polistirene Mn =1.928 MDa e dalla tenacità delle catene N =250, rispettivamente. Credito: Progressi scientifici , 10.1126/sciadv.abg9763
Proprietà meccaniche delle miscele polimeriche e conteggio degli entanglement
Bukowsky et al. regolato il numero di entanglement nel sistema mescolando polimeri monodispersi della stessa struttura chimica. Questo metodo ha permesso loro di campionare un'ampia gamma di entanglement per catena. Sia gli esperimenti che le simulazioni hanno fornito approfondimenti qualitativi per comprendere in che modo la rete di entanglement ha contribuito alle proprietà meccaniche dei materiali polimerici vetrosi. Durante gli esperimenti, quando la concentrazione delle catene più lunghe diminuisce, anche lo stress massimo e la deformazione da rottura iniziarono a diminuire. Il team ha notato diversi meccanismi di guasto variando il grado di diluizione e dettando il modulo elastico dello stato vetroso del polimero mediante interazioni di intersegmento locali dominate dalle forze di van der Waals. Come Bukowski et al. polimeri a catena lunga integrati, la tenacità misurata nelle simulazioni ha rivelato un aumento monotono.
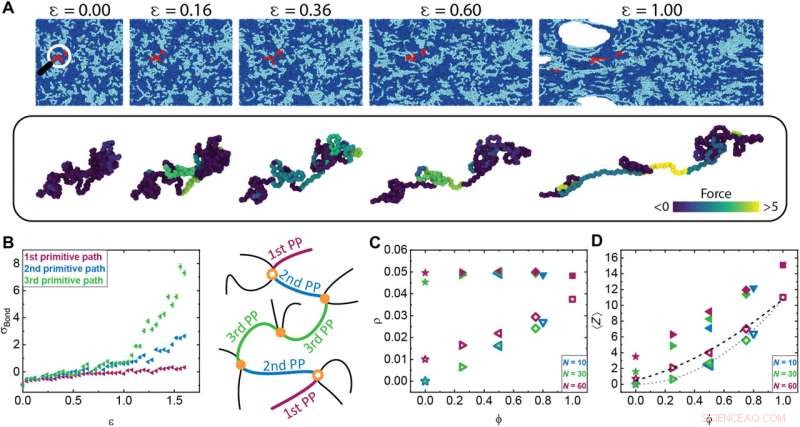
Distribuzione delle forze sugli entanglement. (A) Istantanee di simulazione a vari livelli di deformazione. Una sola catena, evidenziato in rosso nella riga superiore, è mostrato nella riga sottostante in corrispondenza di ciascuno dei ceppi indicati. Le singole catene sono colorate per mostrare vari livelli di stress di legame medio su ciascun percorso primitivo (PP) lungo la catena. (B) La tensione di legame media in funzione della deformazione su ciascun PP in una miscela di N =250 e 30 a ϕ =0,50. Lo schema accanto al grafico delinea dove si trova ciascun PP menzionato. I PP sono codificati a colori per corrispondere ai punti tracciati. Gli entanglement si verificano in corrispondenza di ciascun punto arancione. I punti arancioni vuoti rappresentano gli intrecci non portanti all'estremità delle catene. (C e D) I simboli solidi rappresentano calcoli che considerano tutti gli entanglement nei sistemi blend, e i simboli vuoti considerano solo gli aggrovigliamenti portanti. (C) La densità degli entanglement, , in ogni sistema simulato in funzione della diluizione, calcolato come il numero totale di entanglement diviso per il volume del sistema. Nota che c'è una stella blu fissa nel punto (0, 0). (D) Il numero medio di entanglement per catena, Z⟩, in funzione della diluizione. La linea tratteggiata corrisponde a N =60, e la linea tratteggiata corrisponde a N =30 come catena del diluente. Credito: Progressi scientifici , 10.1126/sciadv.abg9763
Esperimenti e simulazioni
La sollecitazione massima sperimentale e i valori di tenacità simulata sembravano scalare in modo diverso per i diversi modelli sperimentali. I risultati combaciavano bene con un modello fisico introdotto da Mikos e Peppas. Secondo le simulazioni, non tutti gli entanglement in un sistema erano portanti. Dopo, il team ha notato che i ceppi simulati sono molto più grandi di quelli osservati sperimentalmente. Per tenere conto con precisione dei cambiamenti negli intrecci portanti, il team ha considerato il numero medio di entanglement per catena. Bukowsky et al. successivamente ha sviluppato un modello e ha applicato con successo il metodo sia a esperimenti che a simulazioni per studiare la relazione tra gli entanglement e il massimo stress o tenacità. Quando si considera la frazione portante degli impigliamenti nel sistema, gli esperimenti e le simulazioni sono stati scalati in modo simile a livello molecolare. Confrontando successivamente l'esperimento e le simulazioni di sottili film polimerici vetrosi, i dati indicavano un legame quantitativo tra lo stress massimo e la tenacità.
Resistenza e tenacità dei materiali in funzione degli aggrovigliamenti portanti. La normalizzazione è effettuata dallo stress massimo non diluito del polistirene a Mn =1.928 MDa e dalla tenacità non diluita di N =250 per i risultati sperimentali e di simulazione, rispettivamente. I dati sperimentali sono rappresentati da simboli solidi, e i dati di simulazione sono rappresentati da simboli vuoti. Le linee rappresentano il modello Mikos e Peppas modificato calcolato sia per l'esperimento (linea continua) che per la simulazione (linea tratteggiata) includendo solo gli entanglement portanti. Ogni regione ombreggiata rappresenta 1 SD di errore in ogni riga. Lo schema a destra mostra un sistema di intrecci con catene lunghe (blu scuro) e catene corte (azzurro). I punti arancioni solidi rappresentano gli intrecci portanti. I punti vuoti arancioni rappresentano gli entanglement che non possono sopportare il carico perché contengono un primo PP. I punti cavi verdi rappresentano intrecci non portanti realizzati con una specie di catena corta. Le estremità delle catene lunghe sono evidenziate in rosso. Credito: Progressi scientifici , 10.1126/sciadv.abg9763 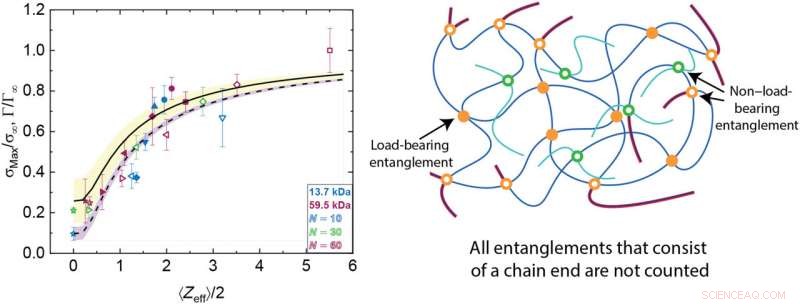
In questo modo, Cynthia Bukowski e colleghi hanno utilizzato una combinazione di esperimenti e simulazioni per mostrare l'importanza di utilizzare intrecci portanti per migliorare la tenacità dei materiali. Per realizzare questo, hanno sistematicamente sintonizzato la densità di entanglement usando miscele bidisperse e chimicamente identiche. Quando hanno aggiunto un diluente a catena corta alle miscele, le prove di trazione del polimero hanno mostrato una diminuzione della sollecitazione massima. Allo stesso modo, la dinamica molecolare delle soluzioni ha anche mostrato una diminuzione della tenacità con l'aggiunta di diluente. Gli esperimenti e le simulazioni combinati hanno fornito una migliore comprensione dei polimeri e una nuova struttura per mettere a punto le proprietà meccaniche in base alla loro composizione molecolare. Il lavoro ha molte implicazioni pratiche oltre a fornire approfondimenti fondamentali sull'origine e la tenacità dei vetri polimerici, comprese le strategie di produzione additiva.
© 2021 Science X Network