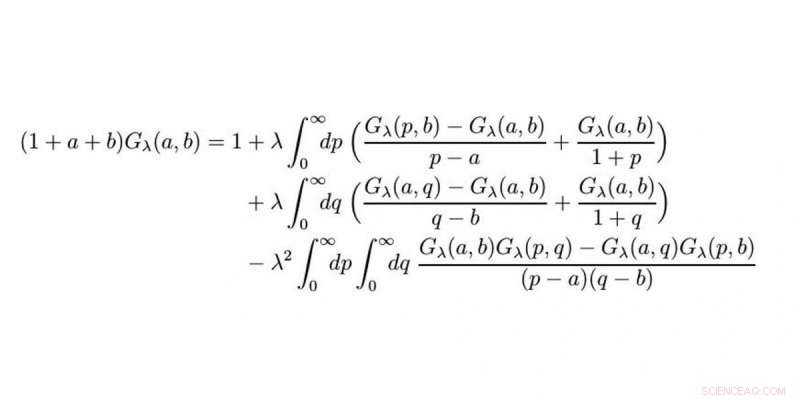
L'equazione matematica. Credito:WWU/Raimar Wulkenhaar
Dopo 10 anni, Il prof. Raimar Wulkenhaar dell'Istituto di matematica dell'Università di Münster e il suo collega Dr. Erik Panzer dell'Università di Oxford hanno risolto un'equazione matematica che era considerata irrisolvibile. L'equazione deve essere utilizzata per trovare le risposte alle domande poste dalla fisica delle particelle elementari. In questa intervista con Christina Heimken, Wulkenhaar ripercorre le sfide incontrate nella ricerca della formula per una soluzione e spiega perché il lavoro non è ancora terminato.
Hai lavorato alla soluzione dell'equazione per 10 anni. Cosa ha reso questa equazione così difficile da risolvere?
È un'equazione integrale non lineare con due variabili. Tale equazione è così complessa che in realtà pensi che non possa esserci alcuna formula per una soluzione. Due variabili da sole sono una sfida in sé, e non ci sono approcci stabiliti per trovare una soluzione per equazioni integrali non lineari. Tuttavia, ancora e ancora durante quei 10 anni ci sono stati barlumi di speranza e, di conseguenza, e nonostante tutte le difficoltà, Pensavo che trovare una formula esplicita per una soluzione, espressa attraverso funzioni note, fosse effettivamente possibile.
Per cosa può essere utilizzata l'equazione?
Si tratta di una comprensione matematica delle teorie quantistiche dei campi. Questi appartengono al campo della fisica e svolgono un ruolo in esperimenti su larga scala come quelli effettuati al CERN. Lo scopo è descrivere matematicamente le particelle elementari, cioè i più piccoli componenti conosciuti della materia. Ma questo è così complicato che, Invece, le particelle immaginarie sono descritte matematicamente che hanno determinate proprietà delle particelle reali. La speranza è che un giorno le particelle reali possano essere descritte utilizzando i metodi stabiliti in questo modo.
Dopo aver lavorato sul problema per 10 anni, hai sperimentato una svolta quest'anno. Come è successo?
Verso la fine di maggio, Ho provato un'idea per la quale il mio dottorato di ricerca. alunno, Alessandro Hock, fornito l'impulso decisivo. Ho elaborato una nuova equazione, più semplice della precedente, e ho iniziato a risolverla in loop. Ciò significa che ti avvicini alla soluzione passo dopo passo, cioè ciclo per ciclo, calcolando il lato sinistro dell'equazione in ogni passaggio precedente e utilizzandolo per il lato destro dell'equazione nel passaggio successivo.
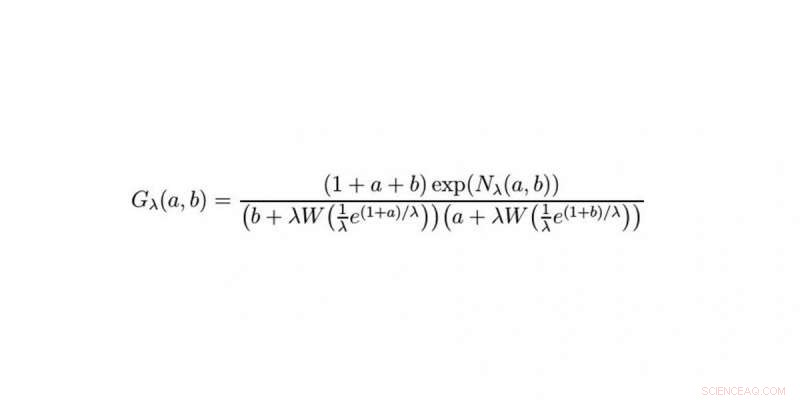
La soluzione. Credito:WWU/Raimar Wulkenhaar
Nel quarto ciclo ho dovuto calcolare una somma di 46 integrali che conteneva tra l'altro polilogaritmi. Questi polilogaritmi, quali sono alcune delle funzioni più impegnative, è diventato più complicato in ogni ciclo. Sono stato fortunato in questo, insomma, quasi tutto è stato cancellato, e ciò che restava era solo una breve somma di potenze dei logaritmi normali. Ho subito capito che c'era un tesoro da trovare qui.
Il quinto loop non è stato così facile da risolvere, ma ancora una volta sono stato fortunato. Durante una scuola estiva nelle Alpi francesi ho avuto l'opportunità di parlare con esperti di tali funzioni. Uno di questi esperti era il dottor Erik Panzer dell'Università di Oxford. Aveva scritto un programma per computer sulla matematica simbolica degli iperlogaritmi e forniva supporto. Durante la notte questo programma ha calcolato la mia equazione fino al settimo ciclo. Ha confermato i miei risultati fino al quarto ciclo, e dopo il quarto ciclo il miracolo continuava:tutto poteva essere scomposto in normali logaritmi. Un modello ha cominciato a emergere!
Che cosa significa?
Forse ricordi il triangolo di Pascal dai tempi della scuola, con i coefficienti binomiali? Nel triangolo, ogni numero inserito in una riga del triangolo è la somma dei due numeri inseriti sopra di essa. Ed è proprio una struttura triangolare del genere che troviamo nei nostri loop, anche se più complicata che nel triangolo di Pascal.
Il 9 giugno, i loop otto e nove sono stati completati. E poi è arrivato quello che forse è stato il momento più importante. Erik Panzer ha decifrato una cosiddetta formula ricorsiva, che genera ogni ultima linea nel triangolo dalla linea sopra di esso, e che ci permette così di estrapolare dal noto all'ignoto.
Cosa ti è passato per la mente in questo momento?
Una delle cose che pensavo era, "Nessuno può essere così fortunato." Ho capito che avremmo risolto l'equazione. Alla nostra cena c'era una bottiglia di vino per la nostra tavola...
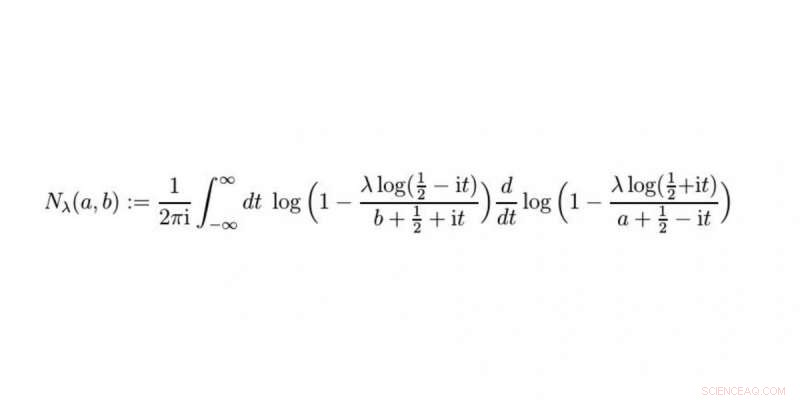
La funzione di Nielsen fa parte della soluzione. Il Prof. Raimar Wulkenhaar e il Dr. Erik Panzer hanno scoperto questa nuova funzione nel corso del loro lavoro. Credito:WWU/Raimar Wulkenhaar
… prima di tornare al lavoro.
Sì. Il giorno dopo riuscii a ridurre parte dell'equazione a una semplice serie di derivate. Inizialmente, il resto sembrava difficile. Solo a tarda sera ebbi l'idea di usare la formula di Cauchy per risolverlo. La mattina dopo ho impostato la sveglia alle 5:30 e l'ho provata subito. Ha funzionato al primo tentativo, e nel passaggio successivo mi sono imbattuto in una formula che avevo visto spesso. Sapevo che sarebbe stato risolto utilizzando la funzione Lambert W. Pochi minuti dopo ho ricevuto una mail da Erik Panzer:anche lui aveva pensato alla funzione Lambert, ma per un percorso completamente diverso. Di conseguenza, abbiamo ottenuto qualcosa che non era stato fattibile per 10 anni:la soluzione dell'equazione integrale che descrive il modello di una teoria quantistica dei campi. È stato semplicemente incredibile.
Utilizzi idee e metodi sviluppati dai matematici nel XVIII secolo che oggi sono stati quasi completamente dimenticati.
Queste vecchie formule ci hanno aiutato molto. La funzione Lambert W, che è una parte elementare della nostra soluzione, prende il nome dal matematico svizzero Johann Heinrich Lambert. Questa equazione si presenta in un gran numero di domande completamente diverse. A causa della mancanza di consapevolezza delle basi di Lambert, la funzione di Lambert è stata inventata più e più volte, ed è stato stabilito come standard solo nel 1993. Abbiamo anche usato la formula di Lagrange-Bürmann, che ci ha aiutato a risolvere un integrale con l'ausilio della funzione Lambert, così come la formula di Cauchy. Generalmente, la matematica ha molto rispetto per i suoi antenati. Nomi come Eulero, Lambert, Lagrange, Cauchy, Gauss e Hilbert sono citati con il massimo riconoscimento per i loro successi. Ma ci sono due strumenti moderni di cui non vorrei fare a meno:Wikipedia e l'algebra informatica. Puoi trovare informazioni complete su Wikipedia che coprono strutture e funzioni matematiche note e meno note. I computer possono risolvere equazioni incomparabilmente più velocemente che a mano, e senza commettere errori
Quali sono i prossimi passi?
Nella nostra soluzione si verifica una nuova funzione che abbiamo chiamato funzione di Nielsen. Quando l'avremo capito meglio e avremo capito, ad esempio, come si collega ad altre funzioni note, sottoporremo il nostro lavoro – che è liberamente accessibile online come prestampa – per la pubblicazione in una rivista specializzata con peer review.
Dopodiché vorrei continuare un lavoro che ho svolto dal 2002 con il mio collega Prof. Harald Grosse di Vienna. Si tratta di una teoria quantistica dei campi per le particelle matematiche. Ora saremo in grado di comprendere appieno questo modello con l'aiuto dell'equazione che abbiamo risolto.