
Se pensavi che le tabelline a scuola fossero difficili, immagina di moltiplicare i numeri con miliardi di cifre. Credito:Shutterstock/Nina Buday
La moltiplicazione di due numeri è facile, Giusto?
Alla scuola primaria impariamo a fare moltiplicazioni lunghe in questo modo:
Metodi simili a questo risalgono a migliaia di anni fa, almeno agli antichi Sumeri ed Egizi.
Ma è davvero questo il modo migliore per moltiplicare due grandi numeri insieme?
Nella moltiplicazione lunga, dobbiamo moltiplicare ogni cifra del primo numero per ogni cifra del secondo numero. Se i due numeri hanno ciascuno n cifre, quello è n 2 (o n X n ) moltiplicazioni del tutto. Nell'esempio sopra, n è 3, e dovevamo fare 3 2 =9 moltiplicazioni.
Intorno al 1956, il famoso matematico sovietico Andrey Kolmogorov ipotizzò che questo fosse il miglior modo possibile per moltiplicare due numeri insieme.
In altre parole, non importa come organizzi i tuoi calcoli, la quantità di lavoro che devi fare sarà almeno proporzionale a n 2 . Il doppio delle cifre significa quattro volte tanto lavoro.
Kolmogorov riteneva che se fosse possibile una scorciatoia, sicuramente sarebbe già stato scoperto. Dopotutto, le persone moltiplicano i numeri da migliaia di anni.
Questo è un superbo esempio dell'errore logico noto come "l'argomento dell'ignoranza".
Un modo più veloce
Solo pochi anni dopo, La congettura di Kolmogorov si dimostrò clamorosamente sbagliata.
Nel 1960, Anatoly Karatsuba, uno studente di matematica di 23 anni in Russia, scoperto un subdolo trucco algebrico che riduce il numero di moltiplicazioni necessarie.
Per esempio, moltiplicare i numeri a quattro cifre, invece di aver bisogno di 4 2 =16 moltiplicazioni, Il metodo di Karatsuba se la cava con solo nove. Quando usa il suo metodo, il doppio delle cifre significa solo tre volte tanto lavoro.
Questo si accumula fino a un vantaggio impressionante man mano che i numeri aumentano. Per i numeri con mille cifre, Il metodo di Karatsuba richiede circa 17 volte meno moltiplicazioni rispetto alla moltiplicazione lunga.
Ma perché mai qualcuno dovrebbe voler moltiplicare insieme numeri così grandi?
Infatti, ci sono un numero enorme di applicazioni. Uno dei più visibili ed economicamente significativi è nella crittografia.
Grandi numeri nella vita reale
Ogni volta che ti impegni in una comunicazione crittografata su Internet, ad esempio, accedi al tuo sito Web bancario o esegui una ricerca sul Web:il tuo dispositivo esegue un numero da capogiro di moltiplicazioni, coinvolgendo numeri con centinaia o addirittura migliaia di cifre.
Molto probabilmente il tuo dispositivo utilizza il trucco di Karatsuba per questa aritmetica. Tutto questo fa parte dell'incredibile ecosistema software che mantiene il caricamento delle nostre pagine Web il più rapido possibile.
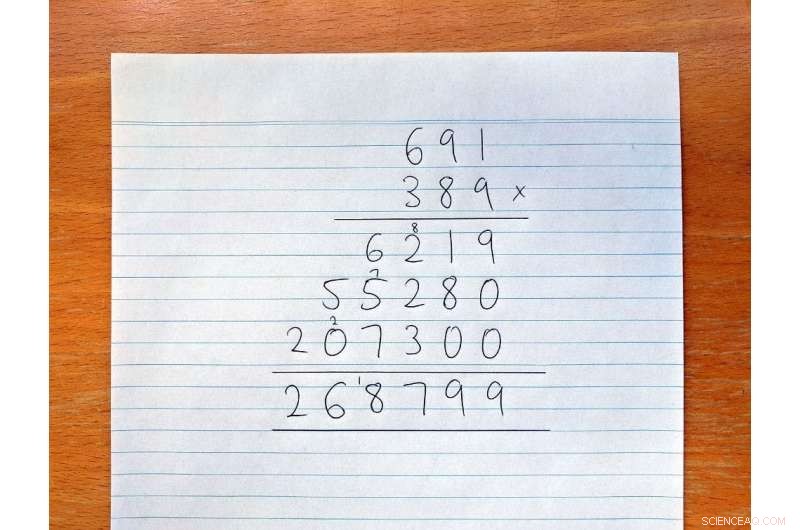
Il lungo cammino verso la moltiplicazione. Credito:David Harvey
Per alcune applicazioni più esoteriche, i matematici hanno a che fare con numeri ancora più grandi, con milioni, miliardi o addirittura trilioni di cifre. Per numeri così enormi, anche l'algoritmo di Karatsuba è troppo lento.
Una vera svolta avvenne nel 1971 con il lavoro dei matematici tedeschi Arnold Schönhage e Volker Strassen. Hanno spiegato come utilizzare la trasformata di Fourier veloce (FFT) pubblicata di recente per moltiplicare in modo efficiente numeri enormi. Il loro metodo è abitualmente utilizzato dai matematici oggi per gestire numeri in miliardi di cifre.
La FFT è uno degli algoritmi più importanti del XX secolo. Un'applicazione familiare nella vita quotidiana è l'audio digitale:ogni volta che ascolti MP3, servizi di streaming musicale o radio digitale, Le FFT gestiscono la decodifica audio dietro le quinte.
Un modo ancora più veloce?
Nel loro articolo del 1971, Anche Schönhage e Strassen fecero una congettura sorprendente. Spiegare, Dovrò essere un po' tecnico per un momento.
La prima metà della loro congettura è che dovrebbe essere possibile moltiplicare n -cifre numeri utilizzando un numero di operazioni di base che è proporzionale al massimo n tronco d'albero ( n ) (quello è n volte il logaritmo naturale di n ).
Il loro algoritmo non ha raggiunto questo obiettivo; erano troppo lenti per un fattore di log (log n ) (il logaritmo del logaritmo di n ). Tuttavia, la loro intuizione li ha portati a sospettare che gli mancasse qualcosa, e quello n tronco d'albero ( n ) dovrebbe essere fattibile.
Nei decenni dal 1971, alcuni ricercatori hanno trovato miglioramenti all'algoritmo di Schönhage e Strassen. In particolare, un algoritmo progettato da Martin Fürer nel 2007 si è avvicinato angosciosamente all'inafferrabile n tronco d'albero ( n ).
La seconda (e molto più difficile) parte della loro congettura è che n tronco d'albero ( n ) dovrebbe essere il limite di velocità fondamentale, che nessun possibile algoritmo di moltiplicazione potrebbe fare meglio di questo.
Suona familiare?
Abbiamo raggiunto il limite?
Poche settimane fa, Io e Joris van der Hoeven abbiamo pubblicato un documento di ricerca che descrive un nuovo algoritmo di moltiplicazione che finalmente raggiunge il n tronco d'albero ( n ) Santo Graal, risolvendo così la parte "facile" della congettura di Schönhage–Strassen.
Il documento non è stato ancora sottoposto a peer review, quindi una certa cautela è giustificata. È pratica standard in matematica diffondere i risultati della ricerca prima che siano stati sottoposti a revisione paritaria.
Invece di utilizzare FFT unidimensionali, la base di tutti i lavori su questo problema dal 1971, il nostro algoritmo si basa su multidimensionale FFT. Questi gadget non sono una novità:il formato immagine JPEG ampiamente utilizzato dipende da FFT bidimensionali, e le FFT tridimensionali hanno molte applicazioni in fisica e ingegneria.
Nel nostro giornale, usiamo FFT con 1, 729 dimensioni. Questo è difficile da visualizzare, ma matematicamente non più problematico del caso bidimensionale.
Veramente, numeri davvero grandi
Il nuovo algoritmo non è realmente pratico nella sua forma attuale, perché la dimostrazione fornita nel nostro articolo funziona solo per numeri ridicolmente grandi. Anche se ogni cifra fosse scritta su un atomo di idrogeno, non ci sarebbe abbastanza spazio disponibile nell'universo osservabile per scriverli.
D'altra parte, speriamo che con ulteriori perfezionamenti, l'algoritmo potrebbe diventare pratico per i numeri con solo miliardi o trilioni di cifre. Se è così, potrebbe diventare uno strumento indispensabile nell'arsenale del matematico computazionale.
Se l'intera congettura di Schönhage-Strassen è corretta, quindi da un punto di vista teorico, il nuovo algoritmo è la fine della strada:non è possibile fare di meglio.
Personalmente, Sarei molto sorpreso se la congettura si rivelasse sbagliata. Ma non dobbiamo dimenticare quello che è successo a Kolmogorov. La matematica a volte può riservare sorprese.
Questo articolo è stato ripubblicato da The Conversation con una licenza Creative Commons. Leggi l'articolo originale. 