Come dimostri qualcosa? Che cos'è la prova?

Nella scienza, la parola "prova" è usata raramente e con grande cura. Gli scienziati accettano che il mondo naturale sia pieno di sorprese, e ciò che sembra essere vero può avere delle eccezioni.

Nei tribunali, la prova spesso include un avvertimento, come "sulla bilancia delle probabilità" per le materie civili, e "al di là di ogni ragionevole dubbio" per i casi penali.

Ma per i matematici come il dottor Nick Beaton dell'Università di Melbourne, Il professor Jan de Gier e il professor Tony Guttmann, "oltre ogni ragionevole dubbio" semplicemente non è abbastanza buono. A loro, una dimostrazione matematica è "al di là di ogni dubbio" ed è una cosa bellissima.

Considera il teorema di Pitagora.

Tutti impariamo a scuola che il quadrato del lato più lungo di un triangolo rettangolo è la somma dei quadrati degli altri due lati. Puoi verificarlo con un pezzo di carta, un righello e una calcolatrice, e vedrai che è vero.

Potresti farlo per mille triangoli e vedrai che è vero per ognuno di quei mille triangoli.

Ma il teorema di Pitagora funziona per ogni possibile triangolo rettangolo?

Non puoi misurare ogni triangolo rettangolo che esiste, quindi il metodo del righello e della calcolatrice non può dimostrare definitivamente che Pitagora ha ragione.

"Fai molte simulazioni e osservi una certa cosa numericamente, e se lo osservassi più e più volte penseresti che probabilmente è sempre così, o è vero, " dice il dottor Nick Beaton.

"Ma non è proprio come avere una dimostrazione matematica in cui puoi effettivamente dimostrare logicamente che una certa cosa accade sempre a determinati valori dei parametri".

Senza una dimostrazione matematica formale, chiamiamo congettura qualcosa come il teorema di Pitagora.

Il professor De Gier dice che una congettura in matematica è un risultato che tutti credono essere vero.

"Ma non è stato dimostrato logicamente in senso rigoroso, " lui dice.

"Così, ci possono essere molte prove numeriche e ci possono essere argomenti forti e convincenti, ma non stanno stabilendo una verità oltre ogni dubbio.

"Un ottimo esempio è l'ipotesi di Riemann sugli zeri della funzione zeta, che è stato controllato per i primi 10, 000, 000, 000, 000 (dieci trilioni) di casi. Manca ancora una prova che sia vero per ogni caso e vale un milione di dollari, "dice il professor De Gier.

"Dimostrare che farebbe luce su molti dei misteri che circondano la distribuzione dei numeri primi".

"E a volte qualcosa sembra molto convincente ma poi viene mostrato, una volta approfonditi nei minimi dettagli, che in realtà non regge e potrebbero esserci delle eccezioni."

Wikipedia ha anche una categoria per "Congetture smentite" - alcune, come la congettura di Eulero, resistette per centinaia di anni prima di essere smentito.

Nel caso del teorema di Pitagora, però, la prova è con noi da migliaia di anni. Infatti, Pitagora non ha inventato la formula, era noto molto prima del suo tempo. Ha escogitato la prima prova nota.

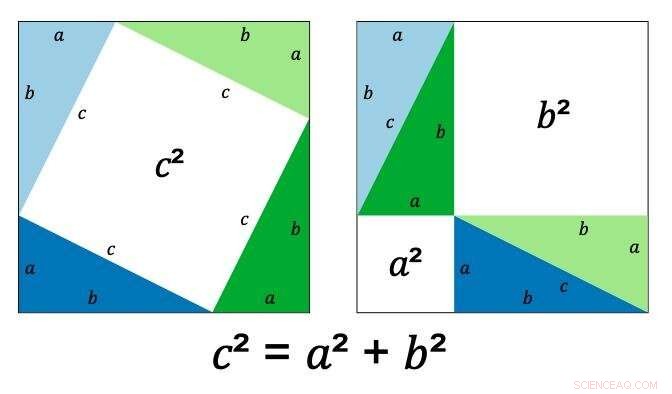
La dimostrazione di Pitagora usa il fatto indiscutibile che ogni triangolo rettangolo può essere rappresentato da due quadrati, uno dentro l'altro, con gli angoli del quadrato interno che toccano il bordo dell'esterno.

Il quadrato interno ha i lati di lunghezza c (la lunghezza effettiva non ha importanza perché c può essere qualsiasi numero positivo), il quadrato esterno ha lunghezza a+b, e il triangolo che fa ha i lati a, b e c (come mostrato).

Modificando l'angolo del quadrato interno si modificano le lunghezze di tutti e tre i valori.

Pitagora dimostrò che riordinando i triangoli all'interno del quadrato, la zona bianca, rappresentato da c² nel diagramma sopra, diventa due quadrati, uno con area a² e uno con area b². Quindi, c² è sempre, non importa quali dimensioni usi, pari a a²+b².

Da Pitagora, i matematici nel corso dei secoli hanno continuato a trovare prove del teorema. Nel 1940, Il matematico americano Elisha Scott Loomis pubblicò una raccolta di dimostrazioni del teorema di Pitagora.

Il team dell'Università di Melbourne non è estraneo alle prove.

L'Australian Mathematical Society ha assegnato il Premio Gavin Brown 2018 per il miglior articolo al Dr. Beaton, Professor de Gier e Professor Guttman, insieme a Mireille Bousquet-Mélou dell'Université de Bordeaux in Francia e Hugo Duminil-Copin dell'Université de Genève in Svizzera, per una prova matematica 2015 dell'esistenza e della tensione superficiale critica per l'adsorbimento di polimeri (molecole a catena lunga) in soluzione.

Il team ha utilizzato una rappresentazione matematica di un polimero, chiamato una "passeggiata auto-evitante, " che sono oggetti usati in una branca della fisica matematica chiamata meccanica statistica.

"Una passeggiata auto-evitante è una passeggiata su un reticolo - molto spesso un reticolo quadrato o un reticolo a nido d'ape - dove non puoi ripercorrere nessuno dei passi che hai fatto, "dice il professor Guttmann.

"Puoi pensare a una passeggiata come a un singolo polimero, con proprietà casuali."

Il dottor Beaton dice che, spesso, trovare una dimostrazione matematica per una congettura è lungo, processo difficile, coinvolgendo tentativi ed errori, lavoro grugnito e l'occasionale momento eureka.

Per Pitagora, il momento eureka era la rappresentazione quadrato in quadrato del triangolo; per il team di Melbourne e i suoi colleghi, era trovare il modo migliore per affrontare matematicamente la casualità.

"La gente ha provato alcune cose quando è stata congetturata per la prima volta, ma nessuno ha fatto molti progressi, quindi era chiaro che era necessaria una nuova idea, ma quale dovesse essere quella nuova idea non era ovvio, "dice il professor De Gier.

Dopo aver seguito alcuni vicoli ciechi, il team si è concentrato su una nuova idea in matematica associata ai modelli reticolari, chiamato "olomorfismo discreto, " che è stato reso popolare dal ricercatore russo Professor Stanislav Smirnov che ha vinto la Medaglia Fields per le eccezionali scoperte in matematica nel 2010.

Usando questo nuovo tipo di matematica, il team di Melbourne ha scoperto che il reticolo a nido d'ape era l'impostazione giusta per dimostrare il problema dei polimeri.

"Per qualche ragione, la matematica delle passeggiate evitanti su un reticolo a nido d'ape ha funzionato bene, "dice il professor de Gier.

"Se vuoi farlo su un reticolo quadrato, non funziona, ma per altri problemi, il reticolo quadrato sarebbe meglio."

Il professor de Gier dice che una dimostrazione matematica non è solo un esercizio intellettuale, può dirci cose fondamentali sulla natura.

"Sapere che qualcosa accade o dove accade è interessante, ma avere quel ragionamento logico è più interessante perché dà un'idea del perché le cose accadono nel modo in cui vanno."