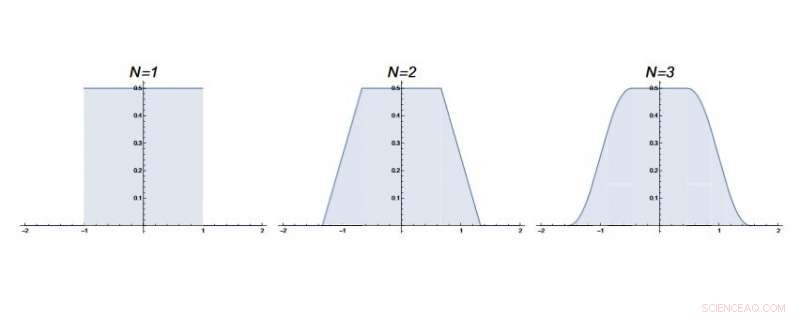
L'"erosione" della densità di probabilità dei camminatori casuali all'origine all'ottavo passo temporale (N ≥ 8, non mostrato) offre alcune intuizioni fisiche sul perché un modello trovato in alcuni integrali di Borwein si rompe improvvisamente nello stesso punto. Credito:Majumdar e Trizac. ©2019 American Physical Society
I modelli appaiono ampiamente in natura e in matematica, dalle spirali di Fibonacci delle conchiglie alla periodicità dei cristalli. Ma alcuni problemi di matematica a volte possono indurre il risolutore umano a vedere uno schema, ma allora, di punto in bianco, il modello scompare improvvisamente. Questi schemi illusori emergono in molte aree della matematica, con un esempio proveniente da certi integrali di calcolo che hanno ingannato l'intuizione anche dei migliori matematici.
Ora in un nuovo studio, due fisici si sono avvicinati a questi integrali utilizzando il concetto fisico di passeggiate casuali. Considerando che la risoluzione di questi integrali di solito richiede un grande sforzo e ingegnosità, i fisici hanno dimostrato che il nuovo approccio può trovare soluzioni in modo intuitivo e talvolta anche senza bisogno di calcoli espliciti.
I fisici Satya N. Majumdar ed Emmanuel Trizac dell'Università di Paris-Sud, CNRS, in Francia, hanno pubblicato un articolo sull'uso dei camminatori casuali per risolvere gli integrali in un recente numero di Lettere di revisione fisica.
"Abbiamo dimostrato che l'intuizione della fisica ci consente di ottenere in modo esente da calcoli una ricchezza di integrali curiosi, e in aggiunta, per ottenere identità precedentemente sconosciute (integrali, o uguaglianze tra somme discrete e integrali), "Trizac ha detto Phys.org . "Il nostro lavoro rivela che quando l'intuizione matematica viene ingannata, l'intuizione fisica può salvare la giornata."
Pattern negli integrali di Borwein
Gli integrali in questione (vedi figura) sono "integrali di Borwein, " prende il nome da David e Jonathan Borwein (padre e figlio), che ha notato in loro schemi insoliti nel 2001. Gli integrali di Borwein coinvolgono il prodotto di funzioni sinc (seno cardinale), che hanno applicazioni diffuse, come nell'ottica, elaborazione del segnale, e altre aree. Questi due particolari integrali possono essere usati per calcolare i volumi degli ipercubi.
Risolvere gli integrali di Borwein comporta la sostituzione dei numeri in per la variabile n . Ogni numero fornisce un valore di soluzione diverso, consentendo ai matematici di osservare modelli nella sequenza di valori risultante. Per esempio, per il primo integrale (I n ), quando sostituisci i numeri n =1-7, ottieni la risposta π ogni volta. Ma quando arrivi a n =8, la risposta è sempre leggermente inferiore a π (circa π – 10 -10 ). La prima volta che i matematici calcolarono questo valore su un computer, pensavano che ci fosse un bug nel software. Ma la risposta è stata confermata, e i termini successivi (per n =9, 10, ecc.) continuano a diventare leggermente più piccoli.

Credito:Majumdar e Trizac. ©2019 American Physical Society
Alcuni modelli persistono anche più a lungo. Per il secondo integrale J n , i primi 56 termini della sequenza (ottenuti sostituendo i numeri da 1 a 56 per n ) sono tutti π/2. Ma il 57 ns il termine è approssimativamente π/2—10 -110 , e i termini successivi continuano a diminuire. (Le cose possono diventare ancora più estreme:per una variante degli integrali di Borwein, non discussa qui, un modello di valore costante vale per un sorprendente primo 10 176 termini della sequenza, dopo di che il modello alla fine si interrompe.)
I matematici possono spiegare perché questi schemi si rompono improvvisamente, almeno in termini matematici. Si noti che entrambi gli integrali di Borwein sopra contengono la funzione sinc(a n K), dove un n =1/(2n—1). Se sostituisci nei numeri 1, 2, 3, … per n in questa espressione, ottieni la sequenza 1, 1/3, 1/5, 1/7, 1/9, ... . I Borwein notarono che il primo termine, 1, non è solo più grande di tutti gli altri termini che seguono, ma è anche più grande della somma dei prossimi termini, dal secondo al settimo termine, per essere precisi, come 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 =0,955… , che è minore di 1. Ma quando si aggiunge l'ottavo termine, 1/15, a questa somma, la risposta è 1.02…, quindi appena sopra 1. Si scopre che non è una coincidenza che il settimo termine sia l'ultimo termine per il quale l'integrale restituisce π, e l'ottavo termine è il punto in cui lo schema si interrompe.
I Borwein hanno dimostrato un teorema (vedi figura) che afferma questa idea in termini più generali. Vale il teorema per il secondo integrale, J n , anche. Contabilità della funzione coseno in J n cambia l'espressione sopra in 2/(2n—1), per la proprietà cos(a)sinc(a) =sinc(2a), in modo che il primo termine sia 2 invece di 1. Come la somma del secondo fino a 56 ns termini dell'espressione è minore di 2, ma aggiungendo il 57 ns termine spinge la somma oltre 2, vale il teorema.
Camminatori casuali
Sebbene il teorema aiuti a spiegare quando i modelli temporanei degli integrali di Borwein si rompono, non è ancora del tutto chiaro perché il teorema sia valido in primo luogo.
Nel nuovo giornale, Majumdar e Trizac hanno offerto alcune intuizioni fisiche al teorema collegandolo ad alcuni concetti ben compresi nella teoria della probabilità e nella meccanica statistica. Hanno notato che l'integrale nel teorema ha stretti legami con la distribuzione di probabilità uniforme, che è ampiamente utilizzato in tutta la scienza. Nello specifico, la trasformata di Fourier della distribuzione di probabilità uniforme sembra essere solo la funzione sinc, che dà l'integrale di Borwein per n =1. Questa connessione collega gli integrali di Borwein al mondo fisico, in modo che utilizzando parametri pertinenti, eventi che seguono una distribuzione uniforme possono essere utilizzati per modellare la sequenza di soluzioni degli integrali di Borwein.
Per descrivere questa connessione in un contesto più fisico, i ricercatori hanno esaminato i camminatori casuali. Un random walker è un oggetto astratto che può spostarsi di una certa distanza in qualsiasi direzione, dove la distanza esatta è scelta casualmente da un intervallo continuo di valori, e ciascuno di questi valori è ugualmente probabile che venga scelto (cioè, segue una distribuzione uniforme). I camminatori casuali possono modellare accuratamente una varietà di fenomeni casuali, come i prezzi di borsa, i sentieri degli animali in cerca di cibo, e i percorsi delle molecole in un gas, che si verificano in uno, Due, o tre dimensioni, rispettivamente.
Nel nuovo giornale, the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. To begin, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).
The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step n corresponds to the solution to the Borwein integral using the same n value.
As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. In realtà, as the maximum distance of each step is restricted, only part of the number line is accessible, cioè., the walkers' world is finite.
Però, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").
But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.
Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. Di conseguenza, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).
By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.
"Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, chimica, biologia, ingegneria, eccetera., " Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future."
© 2019 Scienza X Rete