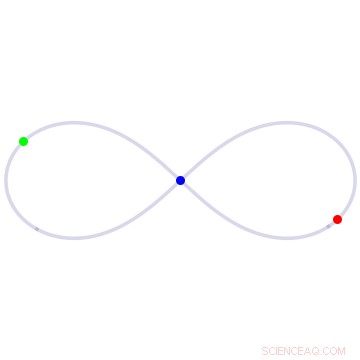
Nella soluzione a otto del problema dei tre corpi, tre corpi di massa uguale si inseguono ciascuno attorno a un anello a forma di otto. Credito:Università della California - Santa Cruz
Dalle sue origini più di 300 anni fa nel lavoro di Newton sulle orbite planetarie, il problema dei tre corpi è sbocciato in un argomento ricco che continua a fornire nuove intuizioni ai matematici.
Richard Montgomery, un illustre professore di matematica all'UC Santa Cruz, lo definisce uno dei classici dilemmi della storia della matematica. In un articolo nel numero di agosto di Scientifico americano , racconta la storia del problema dei tre corpi e i progressi che lui e altri matematici hanno fatto negli ultimi due decenni.
"Ha sfidato le persone per secoli, e questo è in parte ciò che lo rende interessante. Stai aggiungendo al lavoro di persone come Newton, Poincaré e Lagrange, " ha detto Montgomery.
Il problema fondamentale è prevedere i moti di tre corpi (come stelle o pianeti) reciprocamente attratti dalla gravità, date le loro posizioni e velocità iniziali. Risulta che una soluzione generale al problema è essenzialmente impossibile a causa di dinamiche caotiche, che Henri Poincaré scoprì nel 1890.
"Ci sono soluzioni per casi speciali, ma non c'è una formula semplice per darti una soluzione generale, "Spiega Montgomery.
Dal punto di vista pratico della previsione delle orbite planetarie e della pianificazione delle missioni spaziali, le approssimazioni possono essere calcolate con un alto grado di precisione utilizzando computer e un processo chiamato integrazione numerica. Questo potrebbe essere abbastanza buono per la NASA, ma non per i matematici, le cui continue esplorazioni del problema hanno portato a importanti progressi in matematica.
Gatti che cadono
Il problema dei tre corpi lega insieme tre diversi rami della matematica:topologia, geometria, e dinamica. Montgomery ha detto che era ciò che lo interessava più di 20 anni fa. Aveva lavorato su questioni relative alla matematica e alla fisica di come un gatto atterra sui suoi piedi, che ha applicazioni nella teoria del controllo e nell'orientamento dei satelliti.
"Continuavo a semplificare il problema finché il gatto non consisteva di sole tre masse puntiformi, " disse Montgomery. Poi un collega lo indirizzò a un altro matematico che aveva lavorato su idee simili, e in poco tempo era passato dai gatti che cadevano ai meccanici celesti. Sentendo che le persone migliori che lavoravano sulla meccanica celeste erano a Parigi, Montgomery trascorse lì un anno sabbatico lavorando con Alain Chenciner all'Università Diderot di Parigi sul problema dei tre corpi.
Uno dei loro primi grandi risultati, pubblicato nel 2000, è stata una riscoperta e una prova di una soluzione a forma di otto, in cui tre corpi di uguale massa si rincorrono all'infinito attorno ad un anello a forma di otto. Sebbene Chris Moore del Santa Fe Institute avesse trovato per la prima volta questa soluzione nel 1993, utilizzando un metodo di approssimazione numerica, la sua riscoperta da parte di Montgomery e Chenciner ha avuto un impatto molto maggiore sul campo.
"Siamo stati in grado di fornire una prova di esistenza rigorosa della soluzione a otto, e il modo in cui l'abbiamo fatto ha permesso ad altri di generalizzare la soluzione e trovare molte altre cose interessanti, "Spiega Montgomery.
Un'affermazione più generale del problema dei tre corpi per qualsiasi numero di corpi maggiore di due è chiamata problema degli N-corpi. Montgomery ha detto quando ha presentato per la prima volta la soluzione a tre corpi a otto a una conferenza, un membro del pubblico ha subito sottolineato come dovrebbe funzionare per quattro organismi. Prossimamente, i matematici stavano scoprendo una vasta gamma di nuove orbite per il problema di N-corpi di uguale massa. Queste soluzioni periodiche in cui tutte le masse si rincorrono intorno a un punto fisso, curve chiuse senza collisioni furono chiamate "coreografie" dal matematico spagnolo Carles Simó, che ne ha scoperti centinaia.
"Ha creato una mini-industria, così che ora conosciamo un gran numero di queste coreografie, " ha detto Montgomery.
Nuova direzione
Anni dopo, Simó ha aiutato a indirizzare la ricerca di Montgomery sul problema dei tre corpi in una nuova direzione, suggerendogli di cercare i meccanismi dinamici alla base delle soluzioni periodiche. Ciò ha portato a una proficua collaborazione negli ultimi anni con Rick Moeckel dell'Università del Minnesota.
Le nuove idee matematiche emerse dal lavoro di Montgomery sul problema dei tre corpi non hanno applicazioni pratiche, almeno non ancora. Capita spesso che concetti matematici astratti vengano sviluppati molto prima che qualcuno ne trovi un uso pratico.
Molte persone sono rimaste affascinate dal fascino estetico della soluzione a otto e da altre coreografie. Il concetto si è persino fatto strada nella fantascienza grazie all'autore cinese Liu Cixin, il cui romanzo Il problema dei tre corpi ha vinto l'Hugo Award nel 2015.
Ma Montgomery dice che non avrebbe mai affrontato il problema se non fosse stato in carica.
"È un problema così difficile, e non sai se farai progressi, " ha detto. "Ma la persistenza paga a volte. Quindi apprezzo il sistema di possesso, e anche poter prendere anni sabbatici per lavorare con i collaboratori. C'è qualcosa nell'incontrare fisicamente le persone che è così importante per lavorare insieme".
Nel suo Scientifico americano articolo, Montgomery fornisce non solo una descrizione dettagliata del problema dei tre corpi, ma anche un'affascinante storia delle collaborazioni internazionali e dei rapporti personali che gli hanno permesso di fare progressi su questo avvincente enigma matematico.