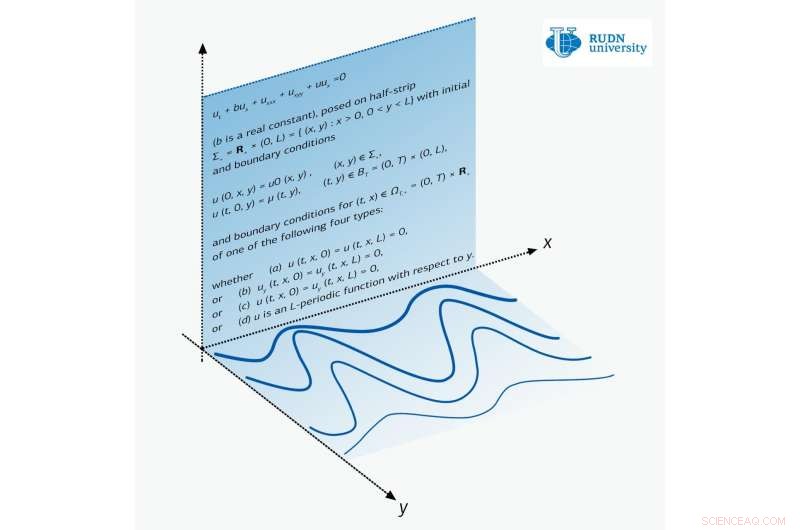
Credito:Università RUDN
Un matematico dell'Università RUDN ha dimostrato per la prima volta il teorema di esistenza e unicità delle soluzioni dell'equazione di Zakharov-Kuznetsov in una striscia. Tali teoremi sono molto rari per le equazioni differenziali alle derivate parziali. I nuovi risultati possono essere applicati in campi come l'astrofisica, ad esempio, nel descrivere la propagazione delle onde piane nel plasma. L'articolo è pubblicato sulla rivista Analisi non lineare:applicazioni del mondo reale .
L'equazione di Zakharov-Kuznetsov è un'equazione a una funzione di due variabili x e y. Per la fisica, x è la direzione di propagazione dell'onda, e la deformazione del mezzo avviene lungo la direzione perpendicolare y. Per esempio, nell'oscillazione di una corda di chitarra, l'onda sembra scorrere lungo la corda, mentre le oscillazioni avvengono perpendicolarmente alla corsa dell'onda.
Ci sono un gran numero di risultati che descrivono soluzioni delle equazioni di Zakharov-Kuznetsov nel caso in cui non ci siano vincoli su y. Ma la questione della propagazione delle onde nella striscia, quando y è limitata, non è stata studiata approfonditamente fino a tempi recenti.
I matematici dell'Università RUDN si sono occupati dell'equazione di Zakharov-Kuznetsov nella striscia. Hanno esaminato tre casi principali:quando non ci sono oscillazioni sul confine della striscia, quando non c'è corrente sullo stesso confine, e quando le condizioni al contorno sono di struttura periodica. Quest'ultimo caso corrisponde alla propagazione delle onde in un mezzo la cui struttura è periodica in x.
In tutti questi casi, i matematici sono riusciti a dimostrare i teoremi dell'esistenza e l'unicità delle loro soluzioni. Per i sistemi di equazioni differenziali alle derivate parziali, che includono l'equazione di Zakharov-Kuznetsov, tali equazioni sono molto rare.
Questi risultati sono i primi per le soluzioni dell'equazione con condizioni iniziali nella striscia. Flussi di plasma piatti con condizioni al contorno, che erano tra i fenomeni considerati dagli scienziati della RUDN University, può verificarsi in fisica e astrofisica.
Le equazioni di Zakharov-Kuznetsov appartengono a una categoria più ampia di equazioni note come equazioni di Korteweg-de Vries. Nello studio di questa categoria di equazioni, è ora possibile descrivere solitoni, onde la cui forma non cambia durante il movimento. I fisici considerano i solitoni come uno strumento per i moderni sistemi di trasmissione dati ottici. Lo studio dei solitoni, che può sorgere nelle equazioni di Zakharov-Kuznetsov, è una delle opzioni per lo sviluppo del lavoro svolto dai matematici dell'Università RUDN.