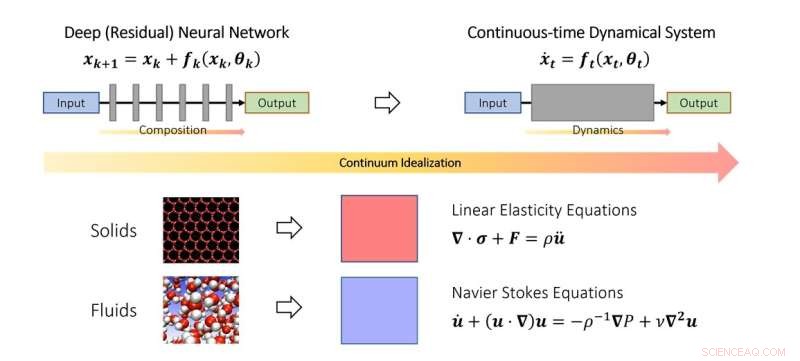
Il punto di vista continuo del deep learning. Simile a come gli scienziati studiano la meccanica dei solidi e dei fluidi nel limite del continuo, si possono anche idealizzare le reti neurali profonde come discretizzazione di un sistema dinamico continuo. Nello schema, il parametro temporale fittizio rappresenta un analogo continuo di strati e la dinamica modella l'impilamento degli strati. Credito:Qianxiao Li
I matematici NUS hanno sviluppato un nuovo quadro teorico basato su sistemi dinamici per capire quando e come una rete neurale profonda può apprendere relazioni arbitrarie.
Nonostante l'ottenimento di un successo diffuso nella pratica, comprendere i principi teorici dell'apprendimento profondo rimane un compito impegnativo. Una delle domande più fondamentali è:le reti neurali profonde possono apprendere relazioni input-output arbitrarie (in matematica, queste sono chiamate funzioni) e il modo in cui raggiungono questo obiettivo differisce dalle metodologie tradizionali?
Per capire questa domanda, è necessario pensare a cosa c'è esattamente di nuovo nelle reti neurali profonde rispetto ai tradizionali paradigmi di approssimazione delle funzioni. Ad esempio, la serie classica di Fourier approssima le funzioni complicate come somma pesata di funzioni più semplici, come seno e coseno. Le reti neurali profonde funzionano in modo molto diverso. Invece di somme ponderate, costruiscono funzioni complesse dall'impilamento ripetuto di funzioni semplici (livelli). Questo è anche noto come composizione di funzioni in matematica. La domanda chiave è come si possono costruire funzioni complicate da quelle semplici impilandole insieme. Si scopre che questo è un problema abbastanza nuovo nel ramo della matematica noto come teoria dell'approssimazione.
In questo studio pubblicato nel Journal of the European Mathematical Society , il professore assistente Qianxiao LI del Dipartimento di Matematica dell'Università Nazionale di Singapore ei suoi collaboratori hanno sviluppato una nuova teoria delle capacità di approssimazione della composizione della funzione. Un'osservazione interessante è che mentre la composizione della funzione è difficile da analizzare in pratica a causa della sua struttura discreta e non lineare, questa non è la prima volta che si verificano tali problemi.
Nello studio del moto di solidi e fluidi, essi sono spesso idealizzati come un continuum di particelle, soddisfacendo alcune equazioni continue (equazioni differenziali ordinarie o alle derivate parziali). Ciò consente di aggirare la difficoltà di modellare tali sistemi a livello atomico discreto. Sono state invece derivate equazioni continue che modellano il loro comportamento a livello macroscopico.
L'idea chiave nello studio è che questo concetto può essere esteso alle reti neurali profonde, idealizzando la struttura a strati come un sistema dinamico continuo. Questo collega l'apprendimento profondo con il ramo della matematica noto come sistemi dinamici. Tali connessioni consentono lo sviluppo di nuovi strumenti per comprendere la matematica dell'apprendimento profondo, inclusa una caratterizzazione generale di quando può effettivamente approssimare relazioni arbitrarie.
Il professor Li ha affermato:"Il punto di vista dei sistemi dinamici dell'apprendimento profondo offre un quadro matematico promettente che mette in evidenza gli aspetti distintivi delle reti neurali profonde rispetto ai paradigmi tradizionali. Ciò porta nuovi entusiasmanti problemi matematici sull'interfaccia dei sistemi dinamici, sulla teoria dell'approssimazione e sull'apprendimento automatico. "
"Un'area promettente di sviluppo futuro consiste nell'estendere questo quadro per studiare altri aspetti delle reti neurali profonde, come ad esempio come addestrarle in modo efficace e come garantire che funzionino meglio su set di dati invisibili", ha aggiunto il prof. Li. + Esplora ulteriormente