
Credito:Università del Connecticut
Chi ha detto che le regole sono fatte per essere infrante non era un fisico. Quando qualcosa non si comporta come pensi che dovrebbe, o le regole sono sbagliate, o c'è una nuova fisica da scoprire. Che è esattamente ciò che Connor Occhialini di UConn, uno studente senior con lode laureandosi in fisica e matematica, trovato quando ha iniziato a fare ricerche sul fluoruro di scandio.
Il fluoruro di scandio è un cristallo trasparente di forma cubica, un sottoprodotto dell'estrazione mineraria. Non è usato commercialmente e non sarebbe particolarmente interessante per nessuno tranne per una cosa strana:si restringe mentre si scalda.
La maggior parte dei materiali si gonfia quando si riscalda. Materiali davvero semplici come il gas idrogeno si gonfiano perché il calore fa girare i loro atomi più velocemente, scontrandosi di più, quindi lo stesso numero di atomi di idrogeno ha bisogno di più spazio. Anche i materiali più complicati si gonfiano, ecco perché la tua porta d'ingresso in legno tende a rimanere attaccata in estate. Ma i solidi come il legno non possono gonfiarsi tanto quanto un gas perché i loro atomi sono strettamente legati tra loro in lunghi, molecole interconnesse, quindi si muovono semplicemente in giro, gonfiando un po' la porta.
Il fluoruro di scandio deve fare qualcos'altro, ragionato Occhialini. Il suo consigliere per il suo progetto di fisica onorificenza, Jason Hancock, aveva lavorato con fluoruro di scandio, e chiese a Occhialini di studiare un modello della dinamica del cristallo. Il fluoruro di scandio ha una struttura piuttosto semplice:è un cristallo solido, con ogni atomo di scandio circondato da sei fluoro per formare pile di ottaedri (diamanti a otto lati). I ricercatori speravano che la semplice struttura potesse essere facile da capire. Comprendere la strana "espansione termica negativa" del fluoruro di scandio, ' come i fisici chiamano il restringimento legato al calore, potrebbe fornire una visione più generale di altri, materiali più complessi che fanno la stessa cosa.

Figura 1. Aiuto, mi sto rimpicciolendo! I diamanti neri rappresentano molecole di fluoruro di scandio. Mentre si scaldano, ruotano, e i contratti di cristallo. Nota come le molecole vicino al centro di massa (punto centrale) si muovono meno delle molecole più vicine al bordo del cristallo. Credito:Università del Connecticut
Il primo passo di Occhialini è stato quello di semplificare il problema. Quindi, invece di un cristallo tridimensionale, decise di pensarlo come un foglio bidimensionale.
Ogni diamante nero rappresenta una molecola di fluoruro di scandio. Gli atomi di scandio (punti blu) sono al centro di ogni diamante, e un atomo di fluoro è ad ogni angolo.
La maggior parte delle volte, i legami tra gli atomi sono flessibili. Quindi in un normale solido cristallino - fluoruro di calcio, per esempio, i fluoro e gli atomi di calcio sarebbero tutti in grado di muoversi indipendentemente quando il materiale si riscaldava. Mentre si muovevano, occuperebbero un po' più di spazio, e il solido si gonfierebbe. Comportamento solido normale.
Ma Occhialini si chiedeva se forse non era quello che stava accadendo nel fluoruro di scandio. Forse in questo modello, avrebbe dovuto presumere che i legami che collegavano ogni fluoro al suo scandio fossero rigidi? Così rigidi che i legami fluoro-scandio non si muovono affatto, quindi i diamanti sono come blocchi solidi. Gli unici punti in cui la struttura potrebbe flettersi quando si riscalda sarebbero gli atomi di fluoro, che agirebbero come piccole giunture. Mentre il cristallo si riscaldava, i piccoli blocchi di fluoruro di scandio si inclineranno intorno ai fluoro agli angoli. Questo è quello che vedi succedere nella foto. Noterai che quando i diamanti si inclinano, l'intera struttura diventa più piccola. In realtà si stringe. Il contorno blu mostra la struttura nel suo momento più freddo, stato perfettamente ordinato, senza movimento molecolare. Quando i diamanti si inclinano, occupano un volume totale inferiore a quello delineato dal contorno blu. Questa è l'espansione termica negativa.
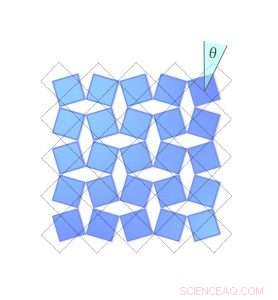
Figura 2. Quanto si restringe un cristallo di fluoruro di scandio dipende da quanto ruotano le molecole. Qui, il diamante blu nell'angolo in alto a destra ruota in senso orario, spazzare un angolo theta. Le linee tratteggiate mostrano la sua posizione quando l'angolo era zero. Credito:Università del Connecticut
Occhialini ha capito che questo ritiro si può descrivere matematicamente, usando solo l'angolo di inclinazione delle molecole. Chiamò l'angolo Θ (theta). Quando i blocchi di fluoruro di scandio si inclinano di un angolo , la distanza tra il centro di ogni blocco si accorcia di un fattore di coseno Θ, e il volume totale del cristallo si riduce.
Per calcolare tale restringimento (o, in un materiale normale, espansione) in dettaglio, Occhialini ha aggiunto un terzo termine alla classica equazione che descrive l'energia di un cristallo vibrante. I primi due termini dell'equazione standard descrivono l'energia potenziale che un cristallo ha dalla flessione a ciascuna giunzione molecolare, più l'energia cinetica di rotazione di ciascuna molecola. L'equazione di Occhialini descrive anche l'energia cinetica traslazionale delle molecole, non solo per la rotazione, ma anche avvicinandosi e allontanandosi dalle loro posizioni originali mentre ruotano. Più sono lontani dal centro di massa del cristallo, più si muovono. Guarda indietro alla Figura 1 e nota il punto nel mezzo; quello è il centro di massa. I diamanti nel mezzo si muovono appena in relazione ad esso, mentre i diamanti ai bordi si muovono molto. Ora immagina quanta differenza ci sarebbe se il cristallo avesse milioni di molecole invece di solo 25. E ora capisci quanto potrebbe essere importante quel terzo termine per l'energia del cristallo.
Ora, le molecole sono molecole, non si restringono e restano lì. si muovono costantemente, e più si scaldano, più si muovono. Parte dell'intuizione di Occhialini è che, in media, la struttura molecolare diventa più flessibile quanto più diventa calda. Quindi le molecole si inclinano di più e trascorrono più tempo a valori maggiori di , più vicino a 45 gradi. Dopo che Occhialini ci ha pensato un po' insieme ad Hancock e ai dottorandi di fisica Sahan Handunkanda ed Erin Curry, si resero conto che c'era una forma geometrica che aveva la stessa descrizione matematica. È il pendolo a spirale di Archimede.
Ogni giro della spirale è esattamente alla stessa distanza dall'ultimo. Quella spaziatura – la distanza tra le spire – è controllata da . Immagina una linea che si estende dal centro della sfera a un punto sulla spirale. L'angolo tra quella linea e il polo della sfera è Θ. Vedi la pallina che viaggia lungo la spirale? Questa è la fine della linea immaginaria. Man mano che diventa più grande, la palla si muove verso l'equatore. Immagina che la palla rappresenti lo stato istantaneo del cristallo di fluoruro di scandio:i fisici hanno calcolato la media statistica di ciò che sta facendo ogni molecola nel cristallo. Noterai che la palla trascorre più tempo vicino all'equatore della sfera a spirale, questo è, tende ad uscire dove è grande. Se la temperatura del cristallo scende e le molecole si muovono meno, diventa più piccolo, più tempo trascorre la pallina vicino al polo della sfera e meno il cristallo si restringe.
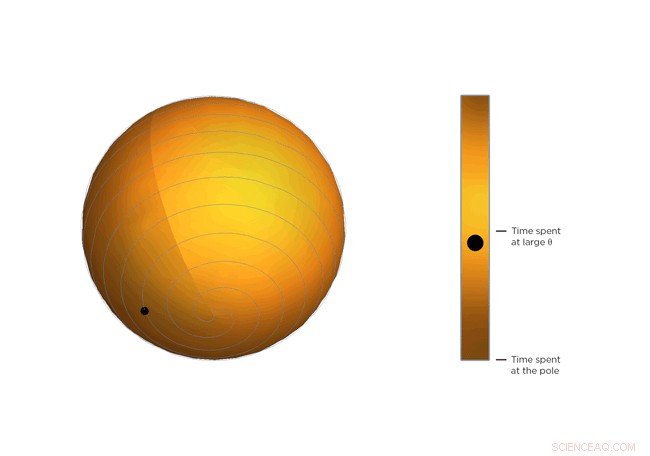
Figura 3. Torcere e restringere. L'equazione che descrive la rotazione delle molecole di fluoruro di scandio è la stessa dell'equazione che descrive il movimento di una palla sul pendolo a spirale di Archimede. Nota come trascorre più tempo ad angoli più ampi. Credito:Università del Connecticut
Quindi non solo un fenomeno davvero strano di un cristallo che si restringe mentre si riscalda può essere spiegato semplicemente assumendo che le molecole siano rigide, ma può essere illustrato con una classica forma geometrica!
Occhialini era solo una matricola quando Hancock lo introdusse al puzzle del fluoruro di scandio. Ha dovuto imparare la matematica mentre andava, ma dopo circa due semestri di lavoro aveva scoperto l'equazione che descriveva cosa stava succedendo. Ora nel suo ultimo anno, dice che le sue esperienze di ricerca nel laboratorio di Hancock sono state parte integrante della sua esperienza di studente universitario.
L'equazione funziona magnificamente e spiega anche alcuni aspetti delle misurazioni sperimentali a raggi X di Hancock.
"Ho imparato molto di più facendo ricerche di quanto qualsiasi corso avrebbe potuto darmi, " dice Occhialini.