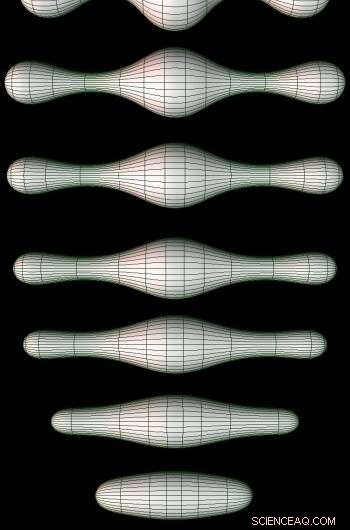
Gli stadi servali di Ricci Flow su una varietà 2D. Credito:https://en.wikipedia.org/wiki/Ricci_flow
La geometria differenziale è lo studio della geometria dello spazio. Molteplici fenomeni naturali, dall'espansione universale all'espansione e contrazione termica, può ricondursi all'evoluzione spaziale. Le due congetture fondamentali in questo campo, la congettura di Hamilton-Tian e il Do parziale 0 congetturare, erano enigmi irrisolti per più di 20 anni.
"La maggior parte dei ciottoli sulla spiaggia sono rotondi. All'inizio potrebbero avere bordi e angoli, ma col passare del tempo e la marea cala e scorre, la loro forma si avvicinerà sempre di più alla perfezione e allo standard. Ma non importa quanto sia perfetta l'evoluzione, potrebbero esserci ancora delle anomalie, che sono chiamate "singolarità" in geometria."
"La congettura di Hamilton-Tian suggerisce che la maggior parte dello spazio è perfetto, mentre la dimensione della "singolarità" può essere limitata a uno spazio a bassa dimensione, " ha detto il prof. Chen Xiuxiong, il fondatore dell'Istituto di Geometria e Fisica, University of Science and Technology of China (USTC) dell'Accademia cinese delle scienze (CAS).
Prof Chen, insieme al Prof. Wang Bing dell'USTC, prima dimostrato le due congetture.
Il loro articolo è stato diviso in 123 pagine in due parti di, il primo dei quali è stato pubblicato nel 2017 e il secondo quest'anno in poi Journal of Differential Geometry , che pubblicò anche il fondamentale lavoro di Hamilton sul flusso di Ricci dopo un lungo corso di cinque anni di sviluppo della teoria e sei anni di peer-review dalla sua prima presentazione.
Questo lavoro ha enfatizzato la teoria della compattezza debole per flussi di Ricci non collassati. Ha introdotto molti pensieri e metodi innovativi, che ha contribuito con implicazioni di vasta portata nel campo dell'analisi geometrica, soprattutto per gli studi sui flussi di Ricci.
Infatti, molti altri lavori sono stati sviluppati sulla base di questo articolo. Per esempio, una nuova soluzione per la stabilità della congettura di Yau basata sulla teoria della struttura dei flussi di Ricci è stata data dal Prof. Chen, Il Prof. Wang e il Dr. Sun Song dell'USTC con la loro derivazione pubblicata in Geometria e Topologia . Prima di ciò, ricevettero il Premio Oswald Veblen in Geometria per la prima soluzione della stabilità della congettura di Yau.
La teoria ei metodi presentati in questo articolo sono stati applicati anche in una serie di lavori del Prof. Wang e dei suoi collaboratori negli ultimi anni.
Le idee centrali di questo articolo sono state generalizzate alla ricerca del flusso di curvatura media dal Prof. Wang e dal Prof. Li Haozhao, che ha risolto il problema dell'estensione, e il risultato è stato pubblicato in Invenzioni matematiche .
L'articolo del Prof. Wang, Il dottor Huang Shaosai e il dottor Li Yu, "Sulla convessità regolare degli spazi limite di Ricci Shrinker, " pubblicato in Diario di Crelle , ha dimostrato che il limite dei solitoni di Ricci che si restringono non collassati deve essere la forma conica definita dal Prof. Chen e dal Prof. Wang.
Inoltre, il documento "Heat Kernel on Ricci Shrinkers, " pubblicato in Calcolo delle variazioni e delle equazioni differenziali parziali dal Prof. Wang e dal Dott. Li, ha sviluppato diverse stime attraverso lo studio del nucleo di calore sui termoretraibili Ricci e ha fornito "strumenti necessari per analizzare le singolarità a breve termine dei flussi di Ricci di dimensione generale".
Questa svolta è stata onorata dal revisore della rivista e dal vincitore di Fields Metal, Prof. Simon Donaldson, chi ha detto, "questo lavoro è un importante passo avanti nell'analisi geometrica, e senza dubbio guiderà molti altri progetti di ricerca correlati".