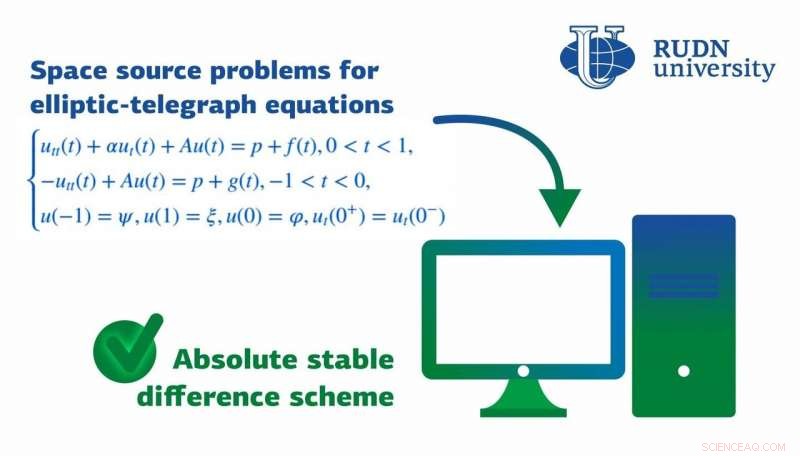
Un matematico della RUDN University ha suggerito uno schema di differenza stabile per risolvere problemi inversi per equazioni telegrafiche ed equazioni differenziali che vengono utilizzate per descrivere fisico, e processi sociologici. I risultati dello studio sono stati pubblicati nel Metodi numerici per equazioni differenziali parziali rivista.

Le equazioni ellittiche sono una classe di equazioni differenziali in derivate parziali che vengono utilizzate, tra l'altro, modellare processi indipendenti dal tempo. Le equazioni del telegrafo sono presentate in una forma non stazionaria. Inizialmente sono stati ottenuti per una linea di comunicazione telegrafica, ma oggi servono anche a modellare il movimento degli insetti, il flusso del sangue nelle vene, e le modifiche subite dai materiali da costruzione. Inoltre, possono essere invertiti, cioè utilizzato per trovare una fonte di modifiche in base a caratteristiche di processo note, Per esempio, per identificare una causa di danno materiale o per creare un'immagine tomografia ottica ai fini della diagnostica medica. Spesso è difficile ottenere soluzioni accurate per problemi come questi; perciò, il problema iniziale si riduce ad un sistema di equazioni più semplici che forniscono una risposta con un certo grado di approssimazione a quella corretta. Un matematico della RUDN University ha suggerito un algoritmo per ottenere soluzioni di problemi inversi per equazioni ellittico-telegrafiche utilizzando un computer.

"Più complesso è un sistema modellato, più parametri sconosciuti contiene, e più difficili sono i calcoli. Però, nonostante la complessità del compito, i computer moderni possono essere utilizzati per cercare soluzioni approssimate alle equazioni differenziali. Si è cercato di ottenere schemi di differenza assoluta stabile per la soluzione approssimata del problema di identificazione dello spazio per le equazioni ellittico-telegrafiche. Il nostro lavoro potrebbe aiutare a implementare ulteriormente questi metodi nella modellazione di vari processi, " ha detto il prof. Allaberen Ashyralyev, un dottorato di ricerca in Fisica e Matematica presso il Dipartimento di Matematica Superiore, Università RUDN.

Un modo per ottenere una soluzione approssimata è sostituire il problema iniziale con schemi di differenza. L'area studiata viene trasformata in una griglia con una data dimensione del passo, e le funzioni vengono sostituite con i valori dei nodi. Il matematico ha suggerito uno schema di differenze e poi lo ha studiato sia analiticamente che numericamente. Il primo metodo è stato utilizzato per confermare l'assoluta stabilità dello schema, e il secondo (un esperimento numerico, cioè un'equazione a cui è stato applicato lo schema) - per supportare i risultati dell'analisi. Lo scienziato è riuscito a dimostrare che lo schema era assolutamente stabile e indipendente dalla dimensione della fase di calcolo scelta.

"Equazioni ellittico-telegrafiche simili sono usate per modellare sistemi biologici, fenomeni sociologici, e processi di ingegneria. Uno schema di differenza assolutamente stabile potrebbe aiutare gli specialisti a studiare meglio questi problemi, " ha aggiunto il Prof. Allaberen Ashyralyev della RUDN University.