
Manoscritto Bakhshali. Credito:Biblioteche di Bodleian, università di Oxford
Non dovrebbe sorprendere che il primo uso registrato del numero zero, recentemente scoperto essere realizzato già nel III o IV secolo, successo in India. La matematica nel subcontinente indiano ha una ricca storia che risale a oltre 3, 000 anni e prosperò per secoli prima che simili progressi fossero fatti in Europa, con la sua influenza estendendosi nel frattempo alla Cina e al Medio Oriente.
Oltre a darci il concetto di zero, I matematici indiani diedero contributi seminali allo studio della trigonometria, algebra, aritmetica e numeri negativi tra le altre aree. Forse più significativamente, il sistema decimale che utilizziamo ancora oggi in tutto il mondo è stato visto per la prima volta in India.
Il sistema dei numeri
Già nel 1200 a.C., la conoscenza matematica veniva scritta come parte di un vasto corpo di conoscenze noto come Veda. In questi testi, i numeri erano comunemente espressi come combinazioni di potenze di dieci. Per esempio, 365 potrebbe essere espresso come trecento (3x10²), sei decine (6x10¹) e cinque unità (5x10⁰), sebbene ogni potenza di dieci fosse rappresentata con un nome piuttosto che con un insieme di simboli. È ragionevole credere che questa rappresentazione con potenze di dieci abbia giocato un ruolo cruciale nello sviluppo del sistema di valori decimali in India.
Dal III secolo a.C., abbiamo anche prove scritte dei numeri Brahmi, i precursori del moderno, Sistema numerico indiano o indo-arabo che la maggior parte del mondo utilizza oggi. Una volta introdotto lo zero, quasi tutti i meccanismi matematici sarebbero stati messi in atto per consentire agli antichi indiani di studiare la matematica superiore.
Il concetto di zero
Lo stesso Zero ha una storia molto più lunga. I primi zeri registrati di recente datazione, in quello che è noto come il manoscritto Bakhshali, erano semplici segnaposto - uno strumento per distinguere 100 da 10. Segni simili erano già stati visti nelle culture babilonese e maya nei primi secoli d.C. e probabilmente nella matematica sumera già nel 3000-2000 aC.
Ma solo in India il simbolo segnaposto del nulla è diventato un numero a sé stante. L'avvento del concetto di zero ha permesso di scrivere i numeri in modo efficiente e affidabile. A sua volta, ciò ha consentito un'efficace tenuta dei registri che significava che importanti calcoli finanziari potevano essere verificati retroattivamente, garantire le azioni oneste di tutti i soggetti coinvolti. Zero è stato un passo significativo sulla strada della democratizzazione della matematica.
Questi strumenti meccanici accessibili per lavorare con concetti matematici, in combinazione con una cultura scolastica e scientifica forte e aperta, significava che, intorno al 600 d.C., tutti gli ingredienti erano a posto per un'esplosione di scoperte matematiche in India. In confronto, questi tipi di strumenti non furono resi popolari in Occidente fino all'inizio del XIII secolo, anche se il libro di Fibonnacci liber abaci.
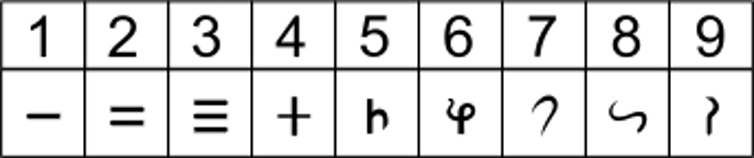
Numeri Brahmi. Credito:Wikimedia
Soluzioni di equazioni quadratiche
Nel VII secolo, le prime prove scritte delle regole per lavorare con lo zero furono formalizzate nel Brahmasputha Siddhanta. Nel suo testo fondamentale, l'astronomo Brahmagupta introdusse regole per risolvere equazioni quadratiche (così amate dagli studenti di matematica delle scuole secondarie) e per calcolare radici quadrate.
Regole per i numeri negativi
Brahmagupta ha anche dimostrato le regole per lavorare con i numeri negativi. Si riferiva ai numeri positivi come fortune e ai numeri negativi come debiti. Scrisse regole come:"Una fortuna sottratta a zero è un debito, " e "un debito sottratto a zero è una fortuna".
Quest'ultima affermazione è la stessa della regola che impariamo a scuola, che se sottrai un numero negativo, è come aggiungere un numero positivo. Brahmagupta sapeva anche che "Il prodotto di un debito e una fortuna è un debito" - un numero positivo moltiplicato per negativo è negativo.
Per la gran parte, I matematici europei erano riluttanti ad accettare i numeri negativi come significativi. Molti ritenevano che i numeri negativi fossero assurdi. Hanno ragionato sul fatto che i numeri sono stati sviluppati per contare e hanno messo in dubbio cosa si potesse contare con numeri negativi. I matematici indiani e cinesi riconobbero presto che l'unica risposta a questa domanda erano i debiti.
Per esempio, in un contesto agricolo primitivo, se un agricoltore deve a un altro agricoltore 7 mucche, quindi effettivamente il primo allevatore ha -7 vacche. Se il primo contadino esce a comprare degli animali per ripagare il suo debito, deve comprare 7 vacche e darle al secondo allevatore per riportare il suo conteggio delle vacche a 0. Da quel momento in poi, ogni vacca che compra va al suo totale positivo.
Base per il calcolo
Questa riluttanza ad adottare numeri negativi, e infatti zero, ha trattenuto la matematica europea per molti anni. Gottfried Wilhelm Leibniz è stato uno dei primi europei a utilizzare lo zero ei negativi in modo sistematico nel suo sviluppo del calcolo alla fine del XVII secolo. Il calcolo viene utilizzato per misurare i tassi di cambiamento ed è importante in quasi ogni branca della scienza, in particolare alla base di molte scoperte chiave nella fisica moderna.
Ma il matematico indiano Bhāskara aveva già scoperto molte delle idee di Leibniz più di 500 anni prima. Bhaskara, ha anche dato importanti contributi all'algebra, aritmetica, geometria e trigonometria. Ha fornito molti risultati, per esempio sulle soluzioni di alcune equazioni "doiphantine", che non sarebbe stato riscoperto in Europa per secoli.
La scuola di astronomia e matematica del Kerala, fondata da Madhava di Sangamagrama nel 1300, è stato responsabile di molti primati in matematica, compreso l'uso dell'induzione matematica e alcuni primi risultati relativi al calcolo. Sebbene la scuola del Kerala non abbia sviluppato regole sistematiche per il calcolo, i suoi sostenitori concepirono per la prima volta molti dei risultati che sarebbero poi stati ripetuti in Europa, comprese le espansioni in serie di Taylor, infinitesimali e differenziazione.
Il balzo, fatto in India, che ha trasformato lo zero da semplice segnaposto a un numero a sé stante indica la cultura matematicamente illuminata che stava fiorendo nel subcontinente in un'epoca in cui l'Europa era bloccata nei secoli bui. Sebbene la sua reputazione soffra del pregiudizio eurocentrico, il subcontinente ha una forte eredità matematica, che continua nel 21° secolo fornendo attori chiave in prima linea in ogni branca della matematica.
Questo articolo è stato originariamente pubblicato su The Conversation. Leggi l'articolo originale. 