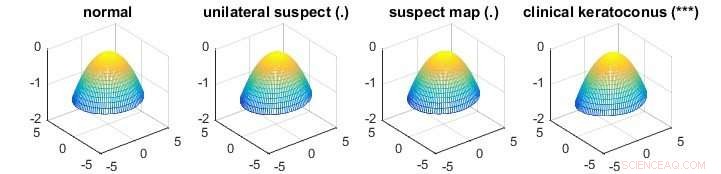
La figura mostra un'applicazione del nuovo metodo nell'identificazione della differenza delle superfici corneali medie con vari gradi della malattia del cheratocono che causano la deformazione delle cornee. I simboli tra parentesi dopo i titoli dei gruppi indicano la significatività statistica della differenza tra il gruppo associato e il gruppo normale, dove "***" indica una differenza altamente significativa e "." suggerisce una differenza non significativa. Il dataset corneale è un esempio di dati ad alta dimensionalità. Il gruppo normale ha 43 superfici corneali mentre il sospetto unilaterale, mappa sospetta, e i gruppi clinici cheratocono hanno 14, 21 e 72 superfici corneali rispettivamente. Ogni superficie corneale ha 6, 912 misurazioni. I tradizionali test MANOVA non sono adatti a questo problema. Credito:Università Nazionale di Singapore
MANOVA (analisi multivariata della varianza) è un metodo statistico comunemente usato nell'analisi dei dati per determinare se c'è qualche differenza nelle medie di diversi gruppi di dati. Però, l'approccio classico non è adatto per l'analisi di dati ad alta dimensionalità. I dati ad alta dimensionalità spesso rendono invalidi i tradizionali metodi MANOVA poiché in un MANOVA tradizionale, si assume che la dimensione sia fissa e deve essere molto più piccola del numero di osservazioni. In un ambiente MANOVA ad alta dimensionalità, questo non è più vero. Prof ZHANG Jin-Ting del Dipartimento di Statistica e Probabilità Applicata, NUS e il suo dottorato di ricerca. gli studenti hanno sviluppato un nuovo metodo MANOVA ad alta dimensionalità che può essere utilizzato per confrontare in modo efficiente le medie di diversi gruppi di dati che coinvolgono dati ad alta dimensionalità.
Il nuovo metodo allenta molte condizioni matematiche e restrizioni imposte in letteratura. Uno di questi è il presupposto dell'omoschedasticità. Questa ipotesi è una condizione matematica che richiede che i dati di diversi gruppi abbiano gli stessi modelli di variazione. Il loro nuovo metodo risolve anche i problemi computazionali coinvolti nell'implementazione pratica di MANOVA per dati ad alta dimensionalità. Lo fa utilizzando calcoli di matrice di alto livello computazionalmente efficienti.
Sebbene sia ampiamente applicabile e funzioni bene per molti set di dati della vita reale, il metodo proposto può essere meno efficace in determinate situazioni perché le informazioni di variazione e correlazione delle variabili non sono completamente utilizzate. Quando si analizzano i dati sulla superficie corneale (vedere la figura sotto), viene calcolata la matrice di covarianza associata che contiene le informazioni di variazione e correlazione dai dati. Se il numero di superfici corneali è maggiore del numero di misurazioni di una superficie corneale, la matrice di covarianza calcolata è invertibile, il che significa che la statistica del test può essere ottenuta utilizzando il tradizionale test MANOVA. In un ambiente ad alta dimensione, ciò non è possibile in quanto il numero di superfici corneali (150 =43+14+21+72 campioni) è molto inferiore al numero di misurazioni (6, 912 dimensioni). Però, le informazioni di variazione e correlazione sono ancora parzialmente utilizzate nella stima dei parametri della statistica test. Il professor Zhang e il suo gruppo di ricerca lo stanno studiando per sviluppare metodi statistici migliori in grado di gestire tali situazioni.