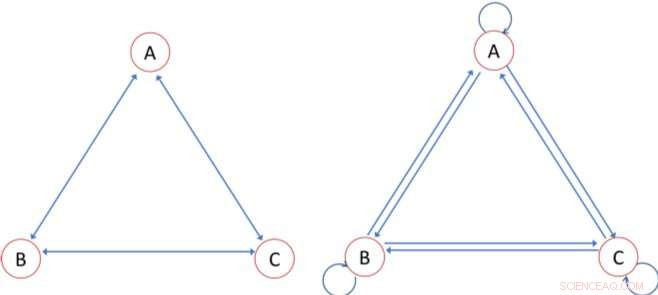
Differenze sperimentate (pannello sinistro) e bordi utilizzati nella misura convenzionale (pannello destro). Se i nodi A, B, e C in Figura 1 hanno ricchezza 10, 4, e 3, Per esempio, il coefficiente di Gini utilizzando la rappresentazione della rete nel pannello di sinistra è 0,412. Usando la rappresentazione di rete a destra, però, il Gini è stimato a 0,274 Credito:Samuel Bowles e Wendy Carlin
Un nuovo modo di misurare la disuguaglianza della ricchezza spiega meglio il modo in cui la viviamo. In un articolo pubblicato su Lettere di Economia , gli economisti Samuel Bowles del Santa Fe Institute e Wendy Carlin dell'University College London e del Santa Fe Institute propongono una nuova svolta sul coefficiente di Gini ampiamente utilizzato, una misura statistica cavallo di battaglia per misurare il divario tra abbienti e non abbienti.
In una società perfettamente egualitaria, dove tutti gli individui sono ugualmente ricchi, il coefficiente di Gini dovrebbe essere 0. Viceversa, una società in cui un singolo individuo detiene tutta la ricchezza dovrebbe avere un coefficiente di Gini uguale a 1. Usando il coefficiente di Gini, i paesi possono essere classificati dal meno al più diseguale.
Ma la ricchezza o il reddito degli individui non è l'intero quadro quando si tratta di disuguaglianza. Secondo Bowles e Carlin, l'algoritmo standard per il calcolo dei coefficienti di Gini produce risultati dispari ad esempio quando un singolo individuo possiede tutta la ricchezza il coefficiente di Gini è inferiore a 1 che è il valore che dovrebbe raggiungere in condizioni di massima disuguaglianza. Correggendo quell'errore, Loro mostrano, richiede una soluzione basata sulla rete che tenga conto delle relazioni tra gli individui nella società.
"Alcune delle dimensioni lungo le quali viene misurata la disuguaglianza sono meglio concepite come attributi individuali, di cui hai semplicemente più o meno, come altezza, " ha spiegato Bowles. "Ma altre dimensioni, come la ricchezza, sono meglio concepite come differenze tra le persone nei loro rapporti con gli altri".
La rete di sinistra nell'immagine rappresenta l'approccio di Bowles e Carlin, dove le frecce che collegano i nodi rappresentano interazioni sociali sperimentate. Con la loro misura, sono le differenze di ricchezza su questi bordi, non la ricchezza di ogni singolo nodo, che è la base della disuguaglianza vissuta. Nella loro carta, Anche Bowles e Carlin che mostrano il corretto coefficiente di Gini si calcola dalle tre differenze associate ai tre spigoli in figura, e la ricchezza media. Per esempio, diciamo che l'individuo A ha una ricchezza di 10, B ha una ricchezza di 4, e C ha una ricchezza di 3. Quindi il coefficiente di Gini correttamente misurato basato sulle differenze lungo i tre bordi nella figura a sinistra è 0,41.
L'algoritmo standard illustrato nel diagramma di destra nell'immagine conta la differenza tra, dire, persona A e B due volte (le due frecce a una punta); ma sorge un errore nell'algoritmo perché conta anche la "differenza" tra la ricchezza di un individuo e la propria ricchezza (le frecce curve), che è sempre zero. Di conseguenza, l'algoritmo standard sottostima il grado di disuguaglianza, ottenendo un coefficiente di Gini di 0,27 per gli stessi dati di cui sopra.
L'errore diventa evidente solo quando si lavora con piccole popolazioni, come fanno spesso archeologi e biologi. Nel caso di Carlin, un gruppo di studenti nella sua classe di economia 101 le ha fatto notare l'errore quando hanno applicato un algoritmo online standard per il calcolo dei coefficienti di Gini a un insieme di problemi.* L'algoritmo che avevano trovato online da Wolfram ha restituito risposte diverse per esempi con un piccolo numero di individui da quelli trovati applicando la definizione che rappresenta il diagramma di rete a sinistra.
Bowles e Carlin usano anche le differenze nella struttura della rete per esaminare l'esperienza della disuguaglianza. Se i tre individui della rete completa (a sinistra) fossero invece riordinati in una linea, con la persona più ricca al centro, come potrebbe rappresentare un padrone di casa con due mezzadri isolati, poi senza mutare la ricchezza dei tre individui, la disuguaglianza sperimentata lungo i bordi che collegano i tre aumenterebbe da 0,41 a 0,57.
Illustrano il loro metodo utilizzando i dati dei social network per stimare la disuguaglianza sperimentata in una comunità di agricoltori in Nicaragua.
"Risolvere il pregiudizio sui piccoli numeri non è il contributo principale del nostro articolo, " dice Carlin. "È che abbiamo fornito un modo di comprendere la disuguaglianza coerente con le nostre intuizioni su come viviamo le disparità economiche, cioè confrontando a due a due la propria ricchezza o il proprio reddito con quello degli altri".