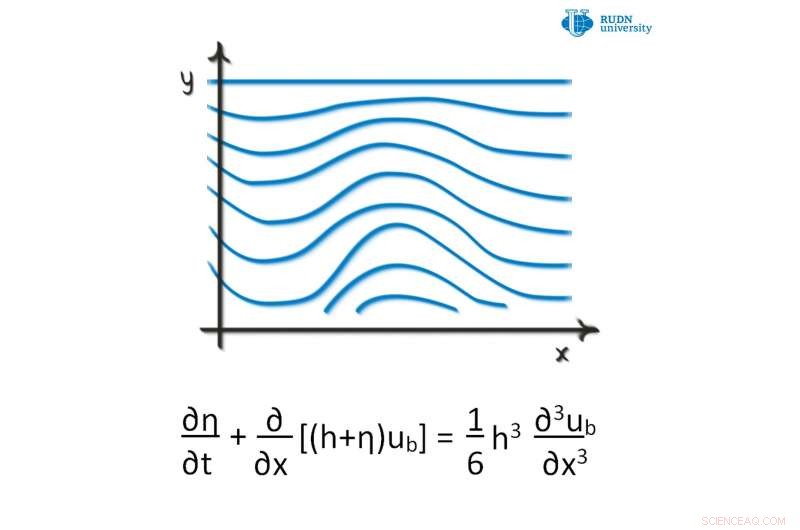
Credito:Università RUDN
Un matematico dell'Università RUDN ha proposto un nuovo criterio per risolvere le equazioni di Boussinesq. Queste equazioni descrivono la propagazione non lineare delle onde in determinati mezzi, per esempio. plasma, una superficie di liquido di bassa profondità, e così via. Hanno esaminato l'equazione di Boussinesq nello spazio tridimensionale e hanno derivato un criterio per l'unicità e l'esistenza di importanti soluzioni di tipo speciale per l'equazione alle derivate parziali di Boussinesq. Il criterio proposto ha applicazioni nella meccanica dei mezzi continui, che studia il moto di liquidi e gas. L'articolo è stato pubblicato su Bollettino della Società Matematica Brasiliana, Nuova serie .
Sia le equazioni di Boussinesq che le equazioni di Navier-Stokes sono sistemi di equazioni alle derivate parziali (la differenziazione viene effettuata rispetto a tutte le variabili indipendenti). Le equazioni alle derivate parziali svolgono un ruolo significativo nella fisica matematica e nella meccanica. Risolvere equazioni di questo tipo è spesso irto di grandi difficoltà. Il problema dell'esistenza e dell'unicità di una soluzione delle equazioni di Boussinesq in determinate condizioni iniziali (il cosiddetto problema di Cauchy) era stato precedentemente studiato da molti scienziati, compresi gli autori dell'articolo. Con determinati valori dei parametri, le equazioni di Boussinesq si trasformano in equazioni di Navier-Stokes. L'esistenza e la differenziabilità continua, o, come dicono i matematici, morbidezza, di soluzioni alle equazioni di Navier-Stokes è uno dei sette problemi del Millennium Prize, posta nel 2000 dal Clay Mathematics Institute.
Per alcuni spazi funzionali (vale a dire, per spazi Besov omogenei, pf di cui i famosi spazi di Sobolev sono un caso speciale), il problema è stato risolto con successo dai matematici Don e Zhang. La matematica dell'Università RUDN Maria Alessandra Ragusa e la sua collega sono andate oltre, dimostrando un criterio simile per le equazioni di Boussinesq in spazi di Besov omogenei. Gli autori hanno esaminato le equazioni di Boussinesq nello spazio tridimensionale, che consente di applicare più pienamente i risultati nelle scienze naturali.
Dopo aver introdotto una serie di definizioni necessarie e dimostrato i lemmi ausiliari, l'autore della RUDN University ha dimostrato con successo il teorema principale e ha mostrato che la soluzione al problema di Cauchy non solo esiste, è unico, e non ha punti singolari, ma si estende anche dolcemente a un intervallo più ampio di una variabile indipendente. L'articolo utilizza l'apparato di analisi funzionale, una disciplina matematica con un alto livello di astrazione. Tuttavia, tali risultati possono trovare ampia e fruttuosa applicazione in meccanica e fisica.