I matematici della RUDN University hanno studiato le proprietà degli operatori compositivi in ​​spazi con norme di Lebesgue miste. Il loro lavoro aiuterà a descrivere la diffusione dei liquidi nei materiali con crepe e nei materiali porosi. Tali spazi sono utili anche per ottenere stime per soluzioni dell'equazione di Navier-Stokes. L'articolo è stato pubblicato su Note matematiche .

La moderna scienza delle equazioni differenziali alle derivate parziali ha una sua teoria:il linguaggio dell'analisi funzionale. Gli studi sugli spazi funzionali in cui si cercano soluzioni alle equazioni sono iniziati nel XIX secolo e sono proseguiti fino ai giorni nostri. All'inizio, i matematici hanno imparato ad applicare la teoria di Fourier alle soluzioni delle più semplici equazioni differenziali alle derivate parziali lineari, poi studiò gli spazi di Banach e Hilbert, così come spazi di funzioni generalizzate, che è essenzialmente il linguaggio della meccanica quantistica.

Verso la metà del XX secolo, Furono scoperti gli spazi di Sobolev; queste occupano ora una delle posizioni centrali nella teoria delle equazioni differenziali alle derivate parziali. Nei prossimi 50 anni, hanno aiutato i matematici a trovare molte soluzioni a problemi applicati che non possono essere trovati negli spazi funzionali ordinari.

Più vicino all'inizio del 21° secolo, è diventato necessario trovare nuovi metodi per studiare le equazioni differenziali alle derivate parziali non lineari, così furono sviluppate la matematica computazionale e la teoria dei sistemi integrabili. Però, metodi di questi campi si sono rivelati troppo ristretti, e la necessità di sviluppare il linguaggio è ancora presente.

Gli spazi di Lebesgue con norme miste sono a volte oggetti più universali e flessibili. Questi spazi sono determinati come segue:Nello spazio delle funzioni in più variabili, definire la norma iterando la norma di Lebesgue. Inizialmente sono sorti come una delle generalizzazioni degli spazi di Sobolev e hanno già attirato molto interesse da parte di teorici di diversi paesi d'Europa, così come la Cina, Canada e Russia.

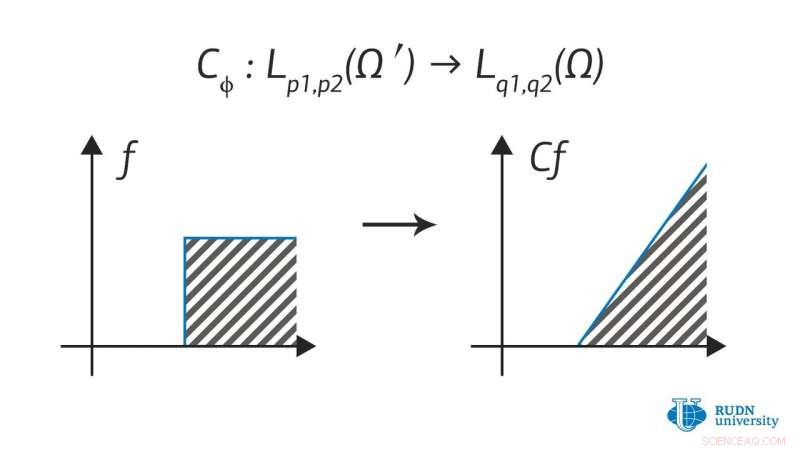
Nikita Evseev e Alexander Menovshchikov dell'Istituto di matematica dell'Università RUDN lavorano su una teoria degli operatori per tali spazi, che ne consente l'utilizzo in problemi applicati formulati nel linguaggio delle equazioni differenziali alle derivate parziali. Hanno prodotto un certo numero di nuovi risultati che descrivono le proprietà degli operatori su tali spazi:criteri per la limitatezza degli operatori, proprietà degli operatori integrali, operatori di moltiplicazione, operatori di composizione, e molti altri. Hanno anche ottenuto alcuni risultati ausiliari utili per l'ulteriore sviluppo di questo campo.

"I nostri metodi e risultati, noi crediamo, può essere applicato a problemi evolutivi e problemi differenziali su regioni non cilindriche. Per esempio, in (matematica) biologia, dove la superficie o l'area oggetto di studio cambia nel tempo, o in idrodinamica, per problemi con bordo variabile, "dice Evseev.

La ricerca in questo campo è utile per studiare le equazioni di Navier-Stokes, un sistema di equazioni che descrivono l'aerodinamica e l'idrodinamica. Gli spazi di Lebesgue a norme miste consentono di valutare soluzioni, quale, a sua volta, permette di prevedere un'assenza di turbolenza, Per esempio.

I risultati aiuteranno anche a studiare i problemi applicati della fisica matematica che sorgono nello studio dei materiali porosi e dei materiali fessurati. Per esempio, sarà possibile prevedere teoricamente il modello di diffusione e trasferimento di calore nei gel di silice, bicchieri porosi, varie spugne, e schiume, così come in alcuni materiali da costruzione.